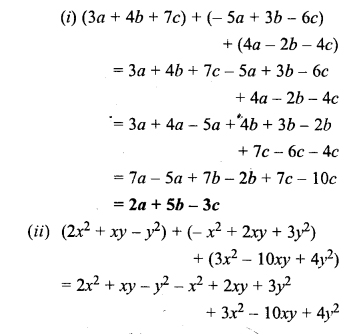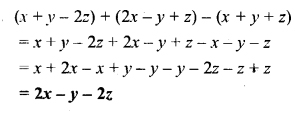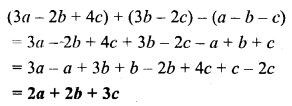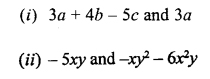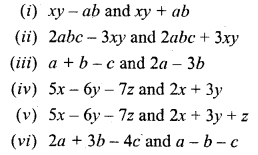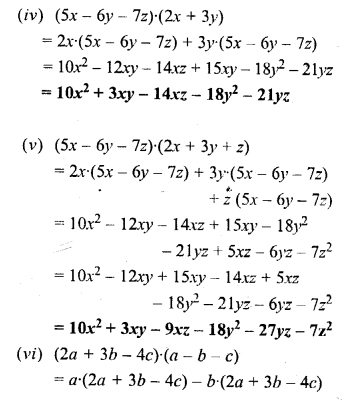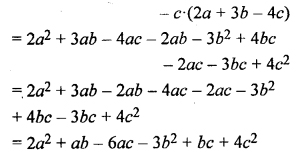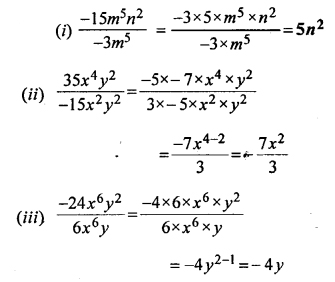Selina Concise Mathematics Class 6 ICSE Solutions Chapter 19 Fundamental Operations

Selina Concise Mathematics Class 6 ICSE Solutions – Fundamental Operations

Selina Concise Mathematics Class 6 ICSE Solutions – Fundamental Operations (Related to Algebraic Expressions)

IMPORTANT POINTS

1. Fundamental Operations : In mathematics, the operations : addition (+), subtraction (-), multiplication (x) and division (÷) are called the four fundamental operations.

2. Addition and Subtraction : 

o Addition of Like Terms : 
 When all the terms are positive, add their coefficients.

 When all the terms are negative, add their coefficients without considering their negative signs and then prefix the minus sign to the sum.

o Addition of Unlike Terms : As discussed above, the sum of two or more like terms is a single like term ; but the two unlike terms cannot be added together to get a single term.

o Subtraction of Like Terms : The same rules, as those for subtraction of integers, are applied for the subraction of like terms. The result of subtraction of two like terms is also a like term.

Add the positive terms together and negative terms separately together. Then, find the result of two terms obtained.

EXERCISE 19(A)

Question 1.
Fill in the blanks :
(i) 5 + 4 = ………… and 5x + 4x = ………….
(ii) 12 + 18 = ………… and 12x2y + 18x2y = ………….
(iii) 7 + 16 = ………….. and 7a + 16b = …………
(iv) 1 + 3 = ………… and x2y + 3xy2 = ………..
(v) 7 – 4 = …………… and 7ab – 4ab = …………..
(vi) 12 – 5 = ………… and 12x – 5y = ……………
(vii) 35 – 16 = ………….. and 35ab – 16ba = ………….
(viii) 28 – 13 = …………. and 28ax2 – 13a2x = ………….
Solution:
(i) 5 + 4 = 9 and 5x + 4x = 9x
(ii) 12 + 18 = 30 and 12x2y + 18x2y = 30x2y
(iii) 7 + 16 = 23 and 7a + 16 b = 7a + 16b
(iv) 1 + 3 = 4 and x2y + 3xy2 = x2y + 3xy2
(v) 7 – 4 = 3 and 7ab – 4ab = 3ab
(vi) 12 – 5 = 7 and 12x – 5y = 12x – 5y
(vii) 35 – 16 = 19 and 35ab – 16ba = 19ab
(viii) 28 – 13 = 15 and 28ax2 – 13a2x = 28ax2 – 13a2x

Question 2.
Fill in the blanks :
(i) The sum of – 2 and – 5 = …………. and the sum of – 2x and – 5x = …………….
(ii) The sum of 8 and – 3 = ………….. and the sum of 8ab and – 3ab = ………….
(iii) The sum of – 15 and – 4 = …………….. and the sum of – 15x and -4y = ………………
(iv) 15 + 8 + 3 = ……….. and 15x + 8y + 3x = …………….
(v) 12 – 9 + 15 = …………… and 12ab – 9ab + 15ba = ……………..
(vi) 25 – 7 – 9 = and 25xy – 7xy – 9yx = ……………
(vii) – 4 – 6 – 5 = …………. and – 4ax – 6ax – 5ay = …………….
Solution:
(i) The sum of – 2 and – 5 = – 7 and the sum of – 2x and – 5x = -7x
(ii) The sum of 8 and -3 = 5 and the sum of 8ab and – 3ab = 5ab
(iii) The sum of – 15 and – 4 = – 19 and the sum of – 15x and – 4y = – 15x – 4y
(iv) 15 + 8 + 3 = 26 and 15x + 8y + 3x = 18x + 8y
(v) 12 – 9 + 15 = 18 and 12ab – 9ab + 15ba = 18ab
(vi) 25 – 7 – 9 = 9 and 25xy – 7xy – 9yx = 9xy
(vii) – 4 – 6 – 5 = – 15 and – 4ax – 6ax – 5ay = – 10ax – 5ay

Question 3.
Add:
(i) 8xy and 3xy
(ii) 2xyz, xyz and 6xyz
(iii) 2a, 3a and 4b
(iv) 3x and 2y
(v) 5m, 3n and 4p
(vi) 6a, 3a and 9ab
(vii) 3p, 4q and 9q
(viii) 5ab, 4ba and 6b
(ix) 50pq, 30pq and 10pr
(x) – 2y, – y and – 3y
(xi) – 3b and – b
(xii) 5b, – 4b and – 10b
(xiii) – 2c, – c and – 5c
Solution:
(i) 8xy + 3xy = 11xy
(ii) 2xyz + xyz + 6xyz = (2 + 1 + 6) xyz = 9xyz

Question 4.

Evaluate :

Solution:
(i) 6a – a – 5a – 2a = 6a – (1 + 5 + 2).a

Question 5.
Evaluate :

Solution:

Question 6.
Subtract the first term from the second :

Solution:

Question 7.
Simplify :

Solution:

EXERCISE 19(B)

Question 1.
Find the sum of :

Solution:

Question 2.
Add the following expressions :

Solution:

Question 3.
Evaluate :

Solution:

Question 4.
Subtract :

Solution:

Question 5.

Solution:

Question 6.
From the sum of x + y – 2z and 2x – y + z subtract x + y + z.
Solution:

Question 7.
From the sum of 3a – 2b + 4c and 3b – 2c subtract a – b – c.
Solution:

Question 8.
Subtract x – 2y – z from the sum of 3x – y + z and x + y – 3z.
Solution:
(3x – y + z) + (x + y – 3 z) – (x – 2y – z)
= 3x – y + z + x + y – 3z – x + 2y + z
= 3x + x – x – y + y + 2y + z + z – 3z
= 3x + 2y – z

Question 9.
Subtract the sum of x + y and x – z from the sum of x – 2z and x + y + z
Solution:

Question 10.
By how much should x + 2y – 3z be increased to get 3x ?
Solution:
3x – (x + 2y – 3z)
= 3x – x – 2y + 3z
= 2x – 2y + 3z

Question 11.

The sum of two expressions is 5x2 – 3y2. If one of them is 3x2 + 4xy – y2, find the other.

Solution:

Question 12.

The sum of two expressions is 3a2 + 2ab – b2. If one of them is 2a2 + 3b2, find the other.

Solution:

 

EXERCISE 19(C)

Question 1.
Fill in the blanks :

Solution:
(i) 6 x 3 = 18 and 6x x 3x = 6 x 3x x x x = 18x2

Question 2.
Fill in the blanks :

Solution:

Question 3.
Find the value of :

Solution:

Question 4.
Multiply :

Solution:

Question 5.
Multiply :

 

Solution:

 
Question 6.
Multiply :

Solution:

Question 7.
Multiply :
(i) x + 2 and x + 10
(ii) x + 5 and x – 3
(iii) x – 5 and x + 3
(iv) x – 5 and x – 3
(v) 2x+ y and x+ 3y
(vi) (3x – 5y) and (x + 6y)
(vii) (x + 9y) and (x – 5y)
(viii) (2x + 5y) and (2x + 5y)
Solution:

Question 8.
Multiply :

Solution:

Question 9.
Find the product of :

Solution:

EXERCISE 19(D)

Question 1.
Divide :

Solution:

Question 2.
Simplify :

Solution:

Question 3.
Divide :

Solution:

 
Question 4.
Simplify :

Solution:

Question 5.
Divide :

Solution: