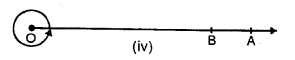Selina Concise Mathematics Class 6 ICSE Solutions Chapter 24 Angles (With their Types)

Selina Concise Mathematics Class 6 ICSE Solutions – Angles (With their Types)

Selina Concise Mathematics Class 6 ICSE Solutions – Angles (With their Types)

IMPORTANT POINTS

1. Ray. A ray is a half-line: It has one end point and other end is open. It can not be measured like a line. Here, OA is a ray.

From appoint, infinite numbers of rays can be drawn.

2. Angle: When two rays meet at a point, then an angle is formed. Angle is measured in degrees with the help of an instrument known as a protractor.

The point where the two rays meet is called an initial point or vertex of the angle and the two rays which form the angle, are called the sides of the angle e.g., two rays OA and OB meet at O.

∴ Angle AOB is formed. Vertex is always kept between the ends points.

The anlgle can be denotes as ∠AOB, or ∠BOA, here sign ‘∠’ denotes the angle.

The angle is also denoted with letters A, B, C etc. or numbers 1, 2, 3 etc. also.

3. Parts of an angl: Angle has three parts : Interior, exterior and the angle itself.

4. Comparison of Angles: Two angles can be compared with respect to their magnitude. Any angle of greater measure is greater.

5. Kinds of Angles : 

(i) Zero angle: When two rotating rays (sides of angles) coincide each other, then ∠ero angle is formed.

(ii) Right angle: An angle of 90° is called a right angle.

(iii) Straight Angle: An angle of 180° is called a straight angle.

(iv) Complete Angle: When a ray completes a revolution on rotating it, then a complete angle is formed.

(v) Acute angle : An angle less than 90° is called an acute angle.

(vi) Obtuse angle : An angle greater than 90° and less than 180° is called an obtuse angle.

  

(vii) Reflex Angle: An angle greater than the 180° and less than 360°

Note:

1 ° = 60 minutes (60′)

1′ = 60 seconds (60″)

6. Pairs of angles :

(i) Adjacent Angles: Two angles with same vertex and one common arm and the other arms lying in opposite sides of it are called adjacent angles, ∠AOB and ∠BOC are adjacent angles.

(ii) Linear Pair: A linear pair is a pair of adjacent angles whose sum is equal to 180°. ∠AOB and ∠BOC are a linear pair as ∠AOB + ∠BOC = 180°.

(iii) Complementary Angle: Two angles whose sum is 90° are called complementary angles. ∠ABC and ∠PQR are complementary angles as ∠ABC + ∠PQR = 30° + 60° = 90°.

(iv) Supplementary Angles: Two angles whose sum is 180°, are called supplementary angles. ∠ABC and ∠PQR are supplementary angles, because

∠ABC + ∠PQR = 130° + 50° = 180°.

(v) Vertically Opposite Angles: When two lines intersect each other, then the pairs of opposite angles so formed are called vertically opposite angles.

∠1 and ∠2 are vertically opposite angles. Similarly, ∠3 and ∠4 are vertically opposite angles.

EXERCISE 24 (A)

Question 1.

For each angle given below, write the name of the vertex, the names of the arms and the name of the angle.

 

Solution:

(i) In figure (i) O is the vertex, OA, OB are its arms and name of the angle is ∠AOB or∠BOA or simply ∠O.

(ii) In figure (ii) Q is the vertex, QP and QR its arms and the name of the angle is ∠PQR or ∠RQP or simply ∠Q.

(iii) In figure (iii), M is the vertex, MN and ML and its anus, and name of the angle is ∠LMN or ∠NML or simply ∠M.

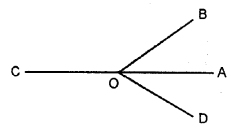
P .Q . Name the angles marked by letters a, b, c, x and y.

Solution:

a = AOE, b = ∠AOB, c = ∠BOC d = ∠COD e= ∠DOE

Question 2.
Name the points :
(i) in the interior of the angle PQR,
(ii) in the exterior of the angle PQR.

Solution:
(i) a, b and x
(ii) d, m, n, s, and t.

Question 3.
In the given figure, figure out the number of angles formed within the arms OA and OE.

 
Solution:
∠AOE, ∠AOD, ∠AOC, ∠AOB, ∠BOC ∠BOD, ∠BOE, ∠COD, ∠COE and ∠DOE.

Question 4.
Add :
(i) 29° 16′ 23″ and 8° 27′ 12″
(ii) 9° 45’56” and 73° 8′ 15″
(m) 56° 38′ and 27° 42’30”
(iv) 47° and 61° 17’4″
Solution:

Question 5.
In the figure, given below name :
(i) three pairs of adjacent angles.
(ii) two acute angles,
(iii) two obtuse angles
(iv) two reflex angles.

Solution:
(i) Three pairs of adjacent angles are
∠AOB and ∠BOC;
∠BOC and ∠COD;
∠COD and ∠DOA.
(ii) Two acute angles are
∠AOB and ∠AOD.
(iii) Two obtuse angles are
∠BOC and ∠COD.
(iv) Two reflex angles are
∠AOB and ∠COD.

Question 6.
In the given figure ; PQR is a straight line. If :
(i) ∠SQR = 75° ; find ∠PQS.
(ii) ∠PQS = 110°; find ∠RQS

Solution:
(i) From figure,
∠PQS + ∠SQR = 180° [Linear pair of angles]
⇒∠PQS + 75° = 180°
⇒ ∠PQS = 180°-75°
⇒ ∠PQS = 105°
(ii) From figure again,
∠PQS + ∠RQS = 180°
⇒ 110° + ∠RQS = 180°
∠RQS = 180°- 110°
∠RQS = 70°

Question 7.
In the given figure ; AOC-is a straight line. If angle AOB = 50°, angle AOE = 90° and angle COD = 25° ; find the measure of :
(i) angle BOC
(ii) angle EOD
(iii) obtuse angle BOD
(iv) reflex angle BOD
(v) reflex angle COE.

Solution:
(i) ∠AOB + ∠BOC = 180° (Linear pairs of angle)
⇒ 50° +∠BOC = 180°
⇒ ∠BOC = 180° – 50° = 130°
⇒ ∠BOC = 130°
(ii) ∠EOD + ∠COD = 90° (∵AOE = 90°)
⇒ ∠EOD + 25° = 90°
⇒ ∠EOD + 25° = 90°
⇒ ∠EOD = 90° – 25°
⇒ ∠EOD = 65°
(iii) ∠BOD = ∠BOC + COD
= 130° + 25° = 155°
(iv) Reflex ∠BOD = 360° – ∠BOD
= 360°- 155° = 205°
(v) Reflex ∠COE = 360° – ∠COE
= 360° (∠COD + ∠EOD)
= 360° – (25° + 65°)
= 360° – 90° = 270°

Question 8.
In the given figure if :
(i) a = 130° ; find b.
(ii) b = 200 ; find a.
(iii) a = 5/3 right angle, find b

Solution:
(i) From figure, a + b = 360°
⇒ 130° + 6 = 360
⇒ 6 = 360°-130°
⇒ b = 230°
(ii) From figure,
a + b = 360°
⇒ a + 200° = 360°
⇒ a = 360° – 200°
⇒ a = 160°
(iii) Here, a=right angle
=x90° = 150°

a = 150°
Here, a + b = 360°
⇒ 150° + b = 360° (∵a = 150°)
⇒ b = 360° -150°
b = 210°

Question 9.
In the given diagram, ABC is a straight line.
(i) If x = 53°, find y.
(ii) If y =1right angles ; find x.

Solution:
(i) From the figure,
∠ABD + ∠DBC = 180° (Linear pair of angles)
⇒ x+y=180°
⇒ 53°+y = 180° (∵ x = 53”)
⇒ y = 180° – 53°
⇒ y = 127°
(ii) From figure again,
x+y= 180°
1 +x 90 = 180°
⇒ x+1right angles = 180°

⇒ x+x90=180°

⇒ x + 135°= 180°
⇒ x= 180° – 135°
⇒ x = 45°

Question 10.

In the given figure, AOB is a straight line. Find the value ofx and also answer each of the following :

(i) ∠AOP = ……..

(ii) ∠BOP = ……..
(iii) which angle is obtuse ?
(iv) which angle is acute ?

Solution:
∠AOP = x + 30°
∠BOP = x – 30°
But ∠AOP + ∠BOP = 180° (∵ ∠AOB is a straight angle)
⇒ x + 30°+x-30° = 180°
⇒ 2x = 180°
⇒ x = 90°
(i) ∠AOP = x + 30° = 90° + 30° = 120°
(ii) ∠BOP = x- 30° = 90° – 30° = 60°
(iii) ∠AOP is an obtuse angle
(iv) ∠BOP is an acute angle

Question 11.
In the given figure, PQR is a straight line. Find x. Then complete the following:
(i) ∠AQB = ……..
(ii) ∠BQP = ……..
(iii) ∠AQR = …….

Solution:
PQR is a straight line
∠AQP=x + 20°
∠AQB = 2x + 10°
∠BQR = x – 10°
But ∠AQP + ∠AQB + ∠BQR = 180°
⇒ x + 20° + 2x + 10° + x-10°= 180°
⇒ 4x + 20°= 180°
⇒4x= 180°-20°= 160°
⇒ x =° = 40°
(i) ∠AQB = 2x + 10° = 2 x 40° + 10° = 80° + 10° = 90°
∠AQP = x + 2(T = 40° + 20° = 60°
∠BQR = x – 10° = 40° – 10° = 30°
(ii) ∠BQP = ∠AQP + ∠AQB = 60° + 90° = 150°
(iii) ∠AQR = ∠AQB + ∠BQR = 90° + 30° = 120°

Question 12.
In the given figure, lines AB and CD intersect at point O.
(i) Find the value of ∠a.
(ii) Name all the pairs of vertically opposite angles.
(iii) Name all the pairs of adjacent angles.
(iv) Name all the reflex angles formed and write the measure of each.

Solution:
Two lines AB and CD intersect each other at O
∠AOC = 68°
(i) ∵ AOB is a line
∠AOC + ∠BOC = 180°
⇒ 68° + a = 180°
⇒ a= 180°-68° = 112°
(ii) ∠AOC and ∠BOD and ∠BOC and ∠AOD are the two pairs of vertically opposite angles .
(iii) ∠AOC and ∠BOC; ∠BOC and ∠BOD; ∠BOD and ∠DOA;
∠DOA and AOC are the pairs of adjacent angles
(iv) ∠BOC and ∠DOA are reflex angles and also ∠AOC and ∠BOD are also reflex angles
Ref. ∠BOC = 180° + 68° = 248°
Ref. ∠DOA = 180° + 68° = 248°
Ref. ∠AOC = 180° + 112° = 292°
and ref. ∠BOD =180° + 112° = 292°

Question 13.
In the given figure :
(i) If ∠AOB = 45°, ∠BOC = 30° and ∠AOD= 110°;
find : angles COD and BOD.
(ii) If ∠BOC = ∠DOC = 34° and ∠AOD = 120° ;
find : angle AOB and angle AOC.
(iii) If ∠AOB = ∠BOC = ∠COD = 38°
find : reflex angle AOC and reflex angle AOD.

Solution:
(i) ∠COD = ∠AOD – ∠AOC
= ∠AOD – (∠AOB + ∠BOC)
= 110°-(45°+ 30°)
= 110°-75° = 35°
∠BOD = ∠AOD -∠AOB
= 110° -45°
= 65°
(ii) ∠AOB = ∠AOD-∠BOD
= ∠AOD – (∠BOC + ∠COD)
= 120° – (34° + 34°)
= 120°-68°
= 52°
∠AOC = ∠AOB + ∠BOC
= 52° + 34°
= 86°
(iii) Reflex ∠AOC = 360°-∠AOC
= 360° – (∠AOB + ∠BOC)
= 360° – (38° + 38°)
= 360° – 76° = 284°
Reflex ∠AOD = 360° – ∠AOD
= 360° (∠AOB + ∠BOC + ∠COD)
= 360° – (38° + 38° + 38°)
= 360°- 114°
= 246°

EXERCISE 24 (B)

Question 1.
Write the complement angle of :
(i) 45°
(ii) x°
(iii) (x – 10)°
(iv) 20° + y°
Solution:
(i) Complement angle of 45°
= 90° – 45° = 45°
(ii) Complement angle of x°
= 90° – x° = (90 – x)°
(iii) Complement angle of (x – 10)° = 90° (x – 10°)
= 90°-x + 10° = 100°-x
(iv) Complement angle of 20° + y°
= 90°-(20°+y°)
= 90° – 20° -y° = 70° -y°

Question 2.
Write the supplement angle of :
(i) 49°
(ii) 111°
(iii) (x – 30)°
(iv) 20° + y°
Solution:
(i) Supplement angle of 49°
= 180°-49° = 131°
(ii) Supplement angle of 111°
= 180°- 1110 = 69°
(iii) Supplment of (x – 30)° = 180° – ( x° – 30°)
= 180o – x° + 30° – 210° – x°
(iv) Supplement of ∠20° + y° = 180° – (20° +y°)
= 180° -20°-y°
= 160° -y°

Question 3.
Write the complement angle of :

Solution:

Question 4.

Solution:

Question 5.
Find the angle :
(i) that is equal to its complement ?
(ii) that is equal to its supplement ?
Solution:
(i) 45° is equal to its complement.
(ii) 90° is equal to its supplement.

Question 6.
Two complementary angles are in the ratio 7 : 8. Find the angles.
Solution:
Let two complementary angles are lx and 8x
∴ 7x + 8x = 90°
⇒ 15x = 90°
⇒ x =°
⇒ x = 6°
∴Two complementary angles are
7x = 7 x 6° = 42°
8x = 8 x 6° = 48°

Question 7.
Two supplementary angles are in the ratio 7 : 11. Find the angles.
Solution:
Let two supplementary angles are 7x and 11x
∴ 7x+ 11x= 180°
⇒ 18x = 180°
⇒ x =
⇒ x = 10°
Two supplementary angles are
7x = 7 x 10° = 70°
11x= 11 x 10°= 110°

Question 8.
The measures of two complementary angles are (2x – 7)° and (x + 4)°. Find x.
Solution:
We know that, sum of two complementary angles = 90°
∴(2x – 7) + (x + 4) = 90°
2x-7 + x + 4 = 90°
⇒ 2x + x – 7 + 4 = 90°
⇒ 3x – 3 = 90°
⇒ 3x = 90 + 3
⇒ 3x = 93
⇒ x =
x = 31

Question 9.
The measures of two supplementary angles are (3x + 15)° and (2x + 5)°. Find x.
Solution:
We know that, sum of two supplementary angles = 180°
∴ (3x + 15)° + (2x + 5)° = 180° ‘
3x + 15 + 2x + 5 = 180°
⇒ 3x + 2x+15 + 5 = 180°
⇒ 5x°+ 20° = 180°
⇒ 5x = 180° – 20°
⇒ 5x= 160°
⇒ x =
⇒ x = 32°

Question 10.
For an angle x°, find :
(i) the complementary angle
(ii) the supplementary angle
(iii) the value of x° if its supplementary angle is three times its complementary angle.
Solution:
For an angle x,
(i) Complementary angle of x° = (90° – x)
(ii) Supplementary angle of x° = (180° – x)
(iii) ∵‘Supplementary angle = 3 (complementary anlge)
180°- x = 3 (90°-x)
⇒ 180°-x = 270°- 3x
⇒-x + 3x = 270°-180°
⇒ 2x = 90°
⇒x== 45°
∴ x = 45°

REVISION EXERCISE

Question 1.
 Explain what do you understand by :
(i) Adjacent angles ?
(ii) Complementary angles ?
(iii) Supplementary angles ?
Solution:

(i) Adjacent Angles:  Two angles are called adjacent angles if (a) they have a common vertex (b) they have one common arm and (iii) the other two arms of the angles are on the opposite sides of the common arm.

(ii) Complementary Angles : Two angles whose sum is 90° are called complementary angles to each other.

(iii) Supplementary Angles : Two angles whose sum.is 180° are called supplementary angles to each other.

Question 2.
Find the value of ‘x’ for each of the following figures :

Solution:

Question 3.

Find the number of degrees in an angle that is (i)of a right angle (ii) 0.2 times of a straight line angle.

Solution:

Question 4.
In the given figure; AB, CD and EF are straight lines. Name the pair of angles forming :
(i) straight line angles.
(ii) vertically opposite angles.

Solution:

In the given figure, AB, CD and EF are straight lines on intersecting, angles are formed a, b, c, d, l, m, n and p.

(i) In the figure pairs of straight line angles are ∠a, ∠b; ∠b, ∠c; ∠c, ∠d; ∠d, ∠a

∠l, ∠m; ∠m, ∠n;∠n, ∠p and ∠p, ∠l

(ii) Pairs of vertically angles are ∠a, ∠c; ∠b, ∠d; ∠l, ∠n; ∠m, ∠p

Question 5.
Find the complement of :

Solution:

Question 6.
Find the supplement of :

Solution:

Question 7.
Two complementary angles are in the ratio 8 : 7. Find the angles.
Solution:

Question 8.
Two supplementary angles are in the ratio 7 : 5. Find the angles.
Solution:

Question 9.
Two supplementary angles are (5x – 82°) and (4x + 73°). Find the value of x.
Solution:

Question 10.
Find the angle formed by the arms of a clock at:
(i) 3 O’clock
(ii) 6 O’clock
(iii) 9 O’clock
(iv) 12 O’clock
Solution:

Question 11.
For an angle y°, find :
(i) its supplementary angle.
(ii) its complementary angle.
(iii) the value of y° if its supplement is four times its complement.
Solution:

Question 12.
Use the adjoining figure to find :
(i) ∠BOD
(ii) ∠AOC
Solution:

Question 13.
Two adjacent angles forming a linear pair are in the ratio 7:5, find the angles.
Solution:

Question 14.
Find the angle that is three times its complementary angle.
Solution:

Question 15.
An angle is one-thirds of a straight line angle ; find :
(i) the angle
(ii) the complement and the supplement of the angle obtained above.
Solution: