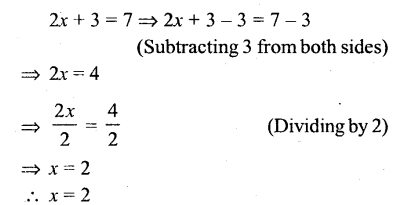Selina Concise Mathematics Class 6 ICSE Solutions Chapter 22 Simple (Linear) Equations (Including Word Problems)

Selina Concise Mathematics Class 6 ICSE Solutions – Simple (Linear) Equations (Including Word Problems)

Selina Concise Mathematics Class 6 ICSE Solutions – Simple (Linear) Equations (Including Word Problems)

IMPORTANT POINTS

1. Simple Equations : A mathematical statement, which states that two expressions are equal, is called simple equation.
2. Properties of Simple Equation :

(i) If same quantity is added to both the sides of simple equation, the sums are equal.

For Example :

x = 6 ⇒ x + a = 6 + a [Adding a on both the sides]

(ii) If same quantity is subtracted from both the sides of simple equation, the remainders are equal.

For Example :

x = 6 ⇒ x-a = 6 – a [Subtracting a on both the sides]

(iii) If both the sides of an equation are multiplied by the same quantity, the products are equal.

For Example :

x = 6 ⇒ a x x = a x 6 i.e. ax = 6a [Multiplying both the sides by a]

(iv) If both the sides of simple equation are divided by the same quantity, the quotients are equal.

For Example :

x = 6 ⇒=
[Dividing both the sides by a]

EXERCISE 22 (A)

Question 1.
Solve:

Solution:

Question 2.
Solve:

Solution:

Question 3.
Solve:

Solution:

Question 4.
Solve:

Solution:

Question 5.
Solve:

 Solution:
 

EXERCISE 22 (B)

Question 1.
Solve:

Solution:

Question 2.
Solve:

Solution:

Question 3.
Solve:

Solution:

EXERCISE 22 (C)

Question 1.
5 – x = 3
Solution:

Question 2.
2 – y = 8
Solution:

Question 3.
8.4 – x = -2
Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.
1.6z = 8
Solution:

Question 8.
3a = – 2.1
Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.
– 5x = 10
Solution:

Question 12.
2.4z = -4.8
Solution:

Question 13.
2y – 5 = -11
Solution:

Question 14.
2x + 4.6 = 8
Solution:

Question 15.
5y – 3.5 = 10
Solution:

Question 16.
3x + 2 = -2.2
Solution:

Question 17.

Solution:

Question 18.

Solution:

Question 19.

Solution:

Question 20.

-3y – 2 = 10
Solution:

Question 21.
4z – 5 = 3 – z
Solution:

Question 22.
7x -3x +2 =22
Solution:

Question 23.
6y + 3 = 2y + 11
Solution:

Question 24.
3 (x+5) = 18
Solution:
3 (x+5) = 18

Question 25.
5 (x-2) -2 (x+2) = 3
Solution:

Question 26.
(5x-3) 4=3
Solution:

Question 27.
3(2x+1) -2(x-5) -5 (5-2x) = 16
Solution:

 

EXERCISE 22 (D)

Question 1.
A number increased by 17 becomes 54. Find the number.
Solution:
Let the required number = x
∴ According to the sum :
x+17 = 54
⇒ x = 54-17
⇒ x = 37
Required number = 37

Question 2.
A number decreased by 8 equals 26, find the number.
Solution:
Let required number = A
∴According to the sum :
x – 8 = 26
⇒A = 26 + 8
⇒A = 34
∴Required number = 34

Question 3.
One-fourth of a number added to two- seventh of it gives 135; find the number.
Solution:

Question 4.
Two-fifths of a number subtracted from three-fourths of it gives 56, find the number.
Solution:

Question 5.

A number is increased by 12 and the new number obtained is multiplied by 5. If the resulting number is 95, find the original number.

Solution:

Question 6.

A number is increased by 26 and the new number obtained is divided by 3. If the resulting number is 18; find the original number.

Solution:

Question 7.

The age of a man is 27 years more than the age of his son. If the sum of their ages is 47 years, find the age of the son and his father.

Solution:

Question 8.

The difference between the ages of Gopal and his father is 26 years. If the sum of their ages is 56 years, find the ages of Gopal and his father.

Solution:

 
Question 9.
When two consecutive natural numbers are added, the sum is 31; find the numbers.
Solution:

Question 10.
When three consecutive natural numbers are added, the sum is 66, find the numbers.
Solution:

Question 11.
A natural number decreased by 7 is 12. Find the number.
Solution:

Question 12.
One fourth of a number added to one- sixth of itself is 15. Find the number.
Solution:

Question 13.
A whole number is increased by 7 and the new number so obtained is multiplied by 5; the result is 45. Find the number.
Solution:

Question 14.
The age of a man and the age of his daughter differ by 23 years and the sum of their ages is 41 years. Find the age of the man.
Solution:

Question 15.
The difference between the ages of a woman and her son is 19 years and the sum of their ages is 37 years; find the age of the son.
Solution:

Question 16.
Two natrual numbers differ by 6 and sum of them is 36. Find the larger number.
Solution:

Question 17.
The difference between two numbers is 15. Taking the smaller number as x; find:
(i) the expression for larger number.
(if) the larger number, if the sum of these numbers is 71.
Solution:

Question 18.

The difference between two numbers is 23. Taking the larger number as x, find:

(i) the expression for smaller number.

(ii) the smaller number, if the sum of these two numbers is 91.

Solution:

Question 19.

Find three consecutive integers such that their sum is 78.

Solution:

Sum of three consecutive numbers = 78

Let first number = x

Then second number = x + 1

and third number = x + 2

Then x + x+1+x + 2 = 78

⇒ 3x + 3 = 78

⇒ 3x = 78 – 3 = 75

⇒ x ==25

∴First number=25

Second number = 25 + 1 = 26

and third number = 26 + 1 = 27

Then the three required numbers are 25, 26,27

Question 20.

The sum of three consecutive numbers is 54. Taking the middle number as x, find:

(i) expression for the smallest number and the largest number.

(ii) the three numbers.

Solution:

Sum of three consecutive numbers = 54

Middle number = x

(i) The first number = x – 1

and third number = x + 1

(ii) ∴x + x-1+x+1 = 54

⇒ 3x = 54

⇒ x== 18

∴First number =18-1 = 17

and third number =18 + 1 = 19

∴Three required numbers are 17, 18,19

REVISION EXERCISE

Question 1.
Solve each of the following equations :
Question i.
2x + 3 = 7
Solution:

Question ii.
2x – 3 = 7
Solution:

Question iii.
2x ÷ 3 = 7
Solution:

Question iv.
3x – 8 = 13
Solution:

Question v.
3y + 8 = 13
Solution:

Question vi.
3y ÷ 8 = 13
Solution:

Question vii.

Solution:

Question viii.

Solution:

Question ix.

Solution:

Question x.
5x – 2.4 = 4.9
Solution:

Question xi.
5y + 4.9 = 2.4
Solution:

Question xii.
48 z + 3.6 = 1.2
Solution:

Question xiii.

Solution:

Question xiv.

Solution:

Question xv.

Solution:

Question xvi.
-3x + 4 = 10
Solution:

Question xvii.
5 = x – 3
Solution:

Question xviii.
8y = 3- 3y
Solution:

Question xix.
4x = 4.9 = 6.5
Solution:

Question xx.
3z + 2 = -4
Solution:

Question xxi.
7y -18 = 17
Solution:

Question xxii.

Solution:

Question xxiii.

Solution:

Question xxiv.

Solution:

Question xxv.
7x -2 = 4x +7
Solution:

Question xxvi.
3y -(y -+2) =4
Solution:

Question xxvii.
3z – 18 = z – (12 -4z)
Solution:

Question xxiii.

Solution:

Question xxix.

Solution:

Question xxx.

Solution:

Question xxxi.
5x – 2x +15 = 27
Solution:

Question xxxii.
5y – 15 = 27 -2y
Solution:

Question xxxiii.
7z + 15 = 3z – 13
Solution:

Question xxxiv.
2 (x -3) – 3 (x-4) =12
Solution:

Question xxxv.
(7y +8) +7= 8
Solution:

Question xxxvi.
2(z-5) +3 (z+2) -(3-5z) =10
Solution:

Question 2.
A natural number decreased by 7 is 12. Find the number.
Solution:

Question 3.
One-fourth of a number added to one-sixth of It is 15. Find the number.
Solution:

Question 4.

A whole number is increased by 7 and the number so obtained is multiplied by 5; the result is 45. Find the whole number.

Solution:

Question 5.

The age of a man and the age of his daughter differ by 23 years and the sum of their ages is 41 years. Find the age of the man.

Solution:

 
Question 6.

The difference between the ages of a woman and her son is 19 years and the sum of their ages is 37 years; find the age of the son.

Solution:

Question 7.
Two natural numbers differ by 6 and their sum is 36. Find the larger number.
Solution:

Question 8.
The difference between two numbers is 15. Taking the smaller number as x; find :
(i) the expression for the larger number.
(ii) the larger number, if the sum of these numbers is 71.
Solution:

Question 9.
The difference between two numbers is 23. Taking the larger number as x, find :
(i) the expression for smaller number.
(ii) the smaller number, if the sum of these two numbers is 91.
Solution:

Question 10.
Find the three consecutive integers whose sum is 78.
Solution:

Question 11.

The sum of three consecutive numbers is 54. Taking the middle number as x, find :

(i) the expressions for the smallest number and the largest number.

(ii) the three numbers.

Solution: