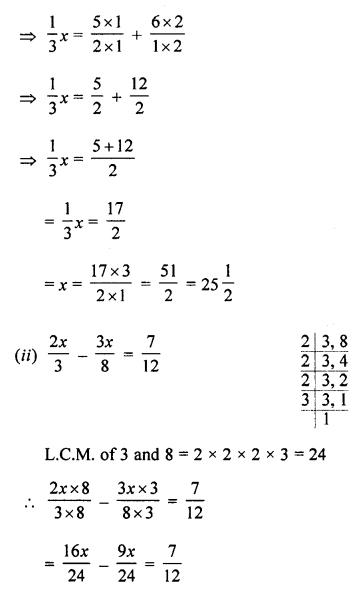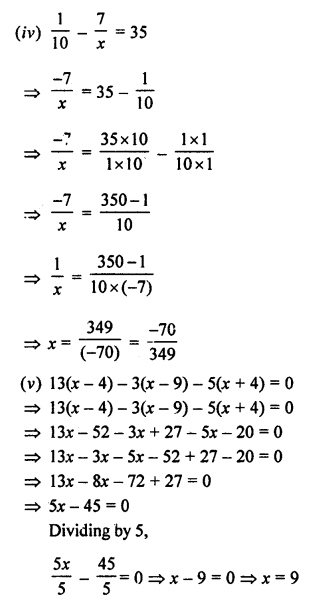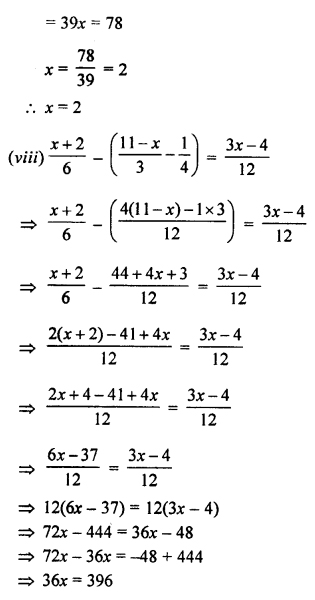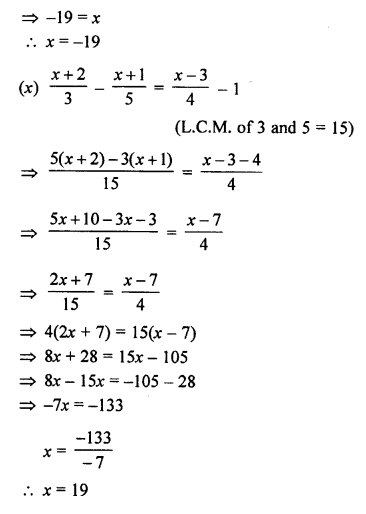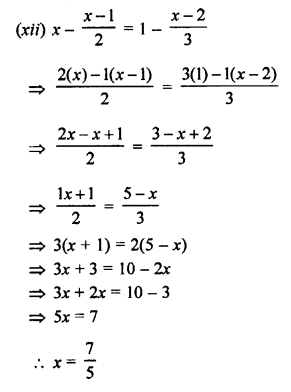Selina Concise Mathematics Class 8 ICSE Solutions Chapter 14 Linear Equations in one Variable

Selina Concise Mathematics Class 8 ICSE Solutions Chapter 14 Linear Equations in one Variable

Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 14 Linear Equations in one Variable (With Problems Based on Linear equations)

Linear Equations in one Variable Exercise 14A – Selina Concise Mathematics Class 8 ICSE Solutions

Solve the following equations:
Question 1.
20 = 6 + 2x
Solution:
20 = 6 + 2x
20 – 6 = 2x
14 = 2x
7 = x
x = 7
Question 2.
15 + x = 5x + 3
Solution:
15 – 3 = 5x – x
12 = 4x
3 = x
x = 3
Question 3.

 = -7
Solution:
3x + 2 = -7 (x – 6) (by cross multiplying)
3x + 2 = -7x + 42
3x + 7x = 42 – 2
10x = 40
x = 4

Question 4.
3a – 4 = 2(4 – a)
Solution:
3a – 4 = 8 – 2a
3a + 2a = 8+4
5a = 12
a = 2.4

Question 5.
3(b – 4) = 2(4 – b)
Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.
5(8x + 3) = 9(4x + 7)
Solution:

Question 9.
3(x +1) = 12 + 4(x – 1)
Solution:
3(x + 1) = 12 + 4(x – 1)
3x + 3 = 12 + 4x – 4
3x – 4x = 12 – 4 – 3
-x = 5
x = -5

Question 10.

Solution:

Question 11.

Solution:

Question 12.

Solution:

Question 13.

Solution:

Question 14.

Solution:

Question 15.

Solution:

Question 16.
6(6x – 5) – 5 (7x – 8) = 12 (4 – x) + 1
Solution:

Question 17.
(x – 5) (x + 3) = (x – 7) (x + 4)
Solution:

Question 18.
(x – 5)2 – (x + 2)2 = -2
Solution:

Question 19.
(x – 1) (x + 6) – (x – 2) (x – 3) = 3
Solution:

Question 20.

Solution:

Question 21.

Solution:

Question 22.

Solution:

Question 23.

Solution:

Question 24.
Solve: 

Hence, find the value of ‘a’, if  + 5x = 8.
Solution:

Question 25.

Solve: 
Hence find the value of ‘p’ if 2p – 2x + 1 = 0
Solution:

Hence x = 8
Now, 3p – 2x + 1=0
⇒ 3p – 2 x 8 + 1 = 0
⇒ 3p – 16 + 1 =0
⇒ 3p – 15 = 0.
⇒ 3p=15
⇒ p = 5

Question 26.
Solve: 
Solution:

Question 27.
Solve: 
Solution:

Linear Equations in one Variable Exercise 14B – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Fifteen less than 4 times a number is 9. Find the number.
Solution:
Let the required number be x
4 times the number = 4x
15 less than 4 times the number = 4x-15
According to the statement :
4x – 15 = 9
⇒ 4x = 9 + 15
⇒ 4x = 24
⇒ x = 6

Question 2.
If Megha’s age is increased by three times her age, the result is 60 years. Find her age
Solution:
Let Megha’s age = x years
Three times Megha’s age = 3x years
According to the statement :
x + 3x = 60
=> 4x = 60
=> x = 15
Megha’s age = 15 years

Question 3.
28 is 12 less than 4 times a number. Find the number.
Solution:
Let the required number be x
4 times the number = 4x
12 less than 4 times the number = 4x – 12
According to the statement
4x – 12 = 28
=> 4x = 28 + 12
=> 4x = 40
x = 10
Required number = 10

Question 4.
Five less than 3 times a number is -20. Find the number.
Solution:
Let the required number = x
3 times the number = 3x
5 less than 3 times the number = 3x – 5
According to statement :
3x – 5 = -20
=> 3x = -20 + 5
=> 3x = -15
=> x = -5
Required number = -5

Question 5.
Fifteen more than 3 times Neetu’s age is the same as 4 times her age. How old is she ?
Solution:
Let Neetu’s age = x years
3 times Neetu’s age = 3x years
Fifteen more than 3 times Neetu’s age = (3x + 15) years
4 times Neetu’s age = 4x
According to the statement :
4x = 3x + 15
=> 4x – 3x = 15
=> x = 15
Neetu’s age = 15 years

Question 6.

A number decreased by 30 is the same as 14 decreased by 3 times the number; Find the number.

Solution:

Let the required number = x
The number decreased by 30 = x – 30
14 decreased by 3 times the number = 14 – 3x
According to the statement :
x – 30 = 14 – 3x
=> x + 3x = 14 + 30
=> 4x = 44
x = 11
Required number =11

Question 7.

A’s salary is same as 4 times B’s salary. If together they earn Rs.3,750 a month, find the salary of each.

Solution:

Let B’s salary = Rs. x
A’s salary = Rs. 4x
According to the statement :
x + 4x = 3750
=> 5x = 3750
=> x = 750
4x = 750 x 4 = 3000
A’s salary = Rs. 3000
B’s salary = Rs. 750

Question 8.
Separate 178 into two parts so that the first part is 8 less than twice the second part.
Solution:
Let first part = x
Second part = 178 – x
According to the problem :
First Part = 8 less than twice the second part
x = 2(178 – x) – 8
=> x = 356 – 2x – 8
=> x+2x = 356 – 8
=> 3x = 348
=> x = 116
First Part = 116
=> Second Part = 178 – x = 178 – 116 = 62
First Part = 116
=> Second Part = 62
Alternative Method :
Let Second part = x
First part = 2x – 8
According to the problem :
x + 2x – 8 = 178
=> x + 2x = 178 + 8
=> 3x = 186
=> x = 62
First part = 2x – 8 = 2 x 62 – 8 = 124 – 8 = 116
First part = 116
Second part = 62

Question 9.
Six more than one-fourth of a number is two-fifth of the number. Find the number.
Solution:
Let the required number = x

x = 40
Required number = 40

Question 10.
The length of a rectangle is twice its width. If its perimeter is 54 cm; find its length.
Solution:
Let width of the rectangle = x cm
Length of the rectangle = 2x cm
Perimeter of the rectangle = 2 [Length + Width] = 2 [2x + x] = 2 x 3x = 6x cm
Given perimeter = 54 cm
6x = 54
=> x = 9
Length = 2x = 2 x 9 = 18 cm

Question 11.

A rectangle’s length is 5 cm less than twice its width. If the length is decreased by 5 cm and width is increased by 2 cm; the perimeter of the resulting rectangle will be 74 cm. Find the length and the width of the origi¬nal rectangle.

Solution:

Let width of the original rectangle = x cm
Length of the original rectangle = (2x – 5)cm
Now, new length of the rectangle = 2x – 5 – 5 = (2x – 10) cm
New width of the rectangle = (x + 2) cm

New perimeter = 2[Length+Width] = 2[2x – 10 + x + 2] = 2[3x – 8] = (6x – 16) cm

Given; new perimeter = 74 cm

6x – 16 = 74
=> 6x = 74 + 16
=> 6x = 90
=>x = 15
Length of the original rectangle = 2x – 5 = 2 x 15 – 5 = 30 – 5 = 25 cm
Width of the original rectangle = x = 15 cm

Question 12.
The sum of three consecutive odd numbers is 57. Find the numbers.
Solution:
Let the three consecutive odd numbers be x, x+2, x+4.
According to the statement :
x + x + 2 + x + 4 = 57
=> x + x + x = 57 – 2 – 4
=> 3x = 51
=> x = 17
Three consecutive odd numbers are 17, 19, 21

Question 13.

A man’s age is three times that of his son, and in twelve years he will be twice as old as his son would be. What are their present ages.

Solution:

Let present age of the son = x years
present age of the man = 3x years
In 12 years :
Son’s age will be = (x + 12) years
The man’s age will be = (3x + 12) years
According to the statement :
3x + 12 = 2(x + 12)
=> 3x + 12 = 2x + 24
=> 3x – 2x = 24 – 12
=> x = 12
3x = 3 x 12 = 36
Hence, present age of the man = 36 years
Present age of the son = 12 years.

Question 14.

A man is 42 years old and his son is 12 years old. In how many years will the age of the son be half the age of the man at that time?

Solution:

Man’s age = 42 years
Son’s age = 12 years
Let after x years the age of the son will be half the age of the man.
Man’s age after x years = (42 + x) years
Son’s age after x years = (12 + x) years
According to the statement :

Hence after 18 years, the age of the son will be half the age of the man

Question 15.

A man completed a trip of 136 km in 8 hours. Some part of the trip was covered at 15 km/hr and the remaining at 18 km/hr. Find the part of the trip covered at 18 km/hr.

Solution:

Question 16.
The difference of two numbers is 3 and the difference of their squares is 69. Find the numbers.
Solution:
Let one number = x
Second number = x + 3 [Difference of two numbers is 3]
According to the statement :

One number = 10
Second number = x + 3 = 10 + 3 = 13

Question 17.

Two consecutive natural numbers are such that one-fourth of the smaller exceeds one-fifth of the greater by 1. Find the numbers.

Solution:

Let two consecutive natural numbers = x, x+1

Two consecutive numbers are 24 and 25

Question 18.

Three consecutive whole numbers are such that if they be divided by 5, 3 and 4 respectively; the sum of the quotients is 40. Find the numbers.

Solution:

Let the three consecutive whole numbers be x, x + 1 and x + 2
According to the statement:

x = 50
x + 1 = 50+1 = 51
x + 2 = 50 + 2 = 52
Three consecutive whole numbers are 50, 51 and 52

Question 19.

If the same number be added to the numbers 5, 11, 15 and 31, the resulting numbers are in proportion. Find the number.

Solution:

Let x be added to each number, then the numbers will be 5 + x, 11 + x, 15 + x and 31 + x

According to the condition

1 should be added

Question 20.

The present age of a man is twice that of his son. Eight years hence, their ages will be in the ratio 7 : 4. Find their present ages.

Solution:

Let present age of son = x year
Then age of his father = 2x
8 years hence,
Age of son = (x + 8) years and age of father = (2x + 8) years
According to the condition,

=> 8x + 32 = 7x + 56
=> 8x – 7x = 56 – 32
=> x = 24
Present age of son = 24 years
and age of father = 2x = 2 x 24 = 48 years
Hence age of man = 48 years and age of his son = 24 years

Linear Equations in one Variable Exercise 14C – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Solve:
(i) 


(ii) 


(iii) (x + 2)(x + 3) + (x – 3)(x – 2) – 2x(x + 1) = 0
(iv) 


(v) 13(x – 4) – 3(x – 9) – 5(x + 4) = 0
(vi) x + 7 – 


(vii) 


(viii) 


(ix) 


(x) 


(xi) 


(xii) 


(xiii) 


(xiv) 


Solution:

Question 2.

After 12 years, I shall be 3 times as old as 1 was 4 years ago. Find my present age.

Solution:

Let present age = x years
According to question,
(x + 12) = 3(x – 4)
x + 12 = 3x – 12
2x = 24
=> x = 12 years
Present age = 12 years

Question 3.

A man sold an article for 7396 and gained 10% on it. Find the cost price of the article

Solution:

S.P. of article = ₹ 396
Gain = 10%
Let cost price = ₹ x

Cost price of an article = ₹ 360

Question 4.

The sum of two numbers is 4500. If 10% of one number is 12.5% of the other, find the numbers.

Solution:

Let the first number = x
and the second number = y
According to question,
x + y = 4500 ……(i)
and 10% x = 12.5% y
i.e. 10x = 12.5y

x = 2500
Hence, the numbers are 2500 and 2000

Question 5.
The sum of two numbers is 405 and their ratio is 8 : 7. Find the numbers.
Solution:
Let the first number = x
and the second number = 7
According to the question, x + y = 405 ……..(i)
and the numbers are in the ratio 8 : 7

x = 189

Hence, the numbers are 189 and 216

Question 6.

The ages of A and B are in the ratio 7 : 5. Ten years hence, the ratio of their ages will be 9 : 7. Find their present ages.

Solution:

Ratio in the present ages of A and B = 7 : 5
Let age of A = 7x years
Let age of B = 5x years
10 years hence,
Then age of A = 7x + 10 years
and age of B = 5x + 10 years
According to the condition,

By crossing multiplication
7(7x + 10) = 9(5x + 10)
=> 49x + 70 = 45x + 90
=> 49x – 45x = 90 – 70
=> 4x = 20
=> x = 5
Present age of A = 7x = 7 x 5 = 35 years
and present age of B = 5x = 5 x 5 = 25 years

Question 7.
Find the number whose double is 45 greater than its half.
Solution:
Let the required number = x
Double of it = 2x

Required number = 30

Question 8.

The difference between the squares of two consecutive numbers is 31. Find the numbers.

Solution:

Let first number = x
and The second number = x + 1
According to the condition,

First number = 15
and second number = 15 + 1 = 16
Hence, the numbers are 15, 16

Question 9.

Find a number such that when 5 is subtracted from 5 times the number, the result is 4 more than twice the number.

Solution:

Let the required number = x
5 times of it = 5x
Twice of it = 2x
According to the condition,
5x – 5 = 2x + 4
=> 5x – 2x = 4 + 5
=> 3x = 9
=> x = 3
Required number = 3

Question 10.

The numerator of a fraction is 5 less than its denominator. If 3 is added to the numerator, and denominator both, the fraction becomes  . Find the original fraction.

Solution:

Let denominator of the original fraction = x
Then numerator = x – 5
  .