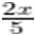Selina Concise Mathematics Class 8 ICSE Solutions Chapter 15 Linear Inequations

 Selina Concise Mathematics Class 8 ICSE Solutions Chapter 15 Linear Inequations

Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 15 Linear Inequations (Including Number Lines)

Linear Inequations Exercise 15A – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
If the replacement set is the set of natural numbers, solve.
(i) x – 5 < 0
(ii) x + 1 < 7
(iii) 3x – 4 > 6
(iv) 4x + 1 > 17
Solution:
(i) x – 5 < 0
x – 5 + 5 <0 + 5 ………(Adding 5)
=> x < 5
Required answer = {1, 2, 3, 4}
(ii) x + 1 ≤ 7 => x + 1 – 1 ≤ 7 – 1 (Subtracting 1)
=> x ≤ 6
Required answer = {1, 2, 3, 4, 5, 6}
(iii) 3x – 4 > 6
3x – 4 + 4 > 6 + 4 (Adding 4)
=> 3x > 10
  > 

 …(Dividing by 3)
=> x > 
=> x > 
Required answer = { 4, 5, 6, …}
(iv) 4x + 1 ≥ 17
=> 4x + 1 – 1 ≥ 17 – 1 (Subtracting)
=> 4x ≥ 16
=>  ≥ 

 (Dividing by 4)
=> x ≥ 4
Required answer = {4, 5, 6, …}

Question 2.
If the replacement set = {-6, -3, 0, 3, 6, 9}; find the truth set of the following:
(i) 2x – 1 > 9
(ii) 3x + 7 < 1
Solution:
(i) 2x – 1 > 9
⇒ 2x – 1 + 1 > 9 + 1 (Adding 1)
⇒ 2x > 10
⇒ x > 5 (Dividing by 2)
⇒ x > 5
Required answer = {6, 9}
(ii) 3x + 7 ≤ 1
⇒ 3x + 7 – 7 ≤ 1 – 7 (Subtracting 7)
⇒ 3x ≤ – 6
⇒ x ≤ – 2
Required Answer = {-6, -3}

Question 3.
Solve 7 > 3x – 8; x ∈ N
Solution:
7 > 3x – 8
=> 7 – 3x > 3x – 3x – 8 (Subtracting 3x)
=> 7 – 7 – 3x > 3x – 3x – 8 – 7 (Subtracting 7)
=> -3x > -15
=> x < 5 (Dividing by -3)
Required Answer = {1, 2, 3, 4}
Note : Division by negative number reverses the inequality.

Question 4.
-17 < 9y – 8 ; y ∈ Z
Solution:
-17 < 9y – 8
=> -17 + 8 < 9y – 8 + 8 (Adding 8)
=> -9 < 9y
=> -1 < y (Dividing by 9)
Required number = {0, 1, 2, 3, 4, …}

Question 5.
Solve 9x – 7 ≤ 28 + 4x; x ∈ W
Solution:
9x – 1 ≤ 28 + 4x
=> 9x – 4x – 7 ≤ 28 + 4x – 4x (Subtracting 4x)
=> 5x – 7 ≤ 28
=> 5x – 7 + 7 ≤ 28 + 7 (Adding 7)
=> 5x ≤ 35
=> x ≤ 7 (Dividing by 5)
Required answer = {0, 1, 2, 3, 4, 5, 6, 7}

Question 6.
Solve : 

 x + 8 < 12 ; x ∈ W
Solution:
 

Question 7.
Solve -5 (x + 4) > 30 ; x ∈ Z
Solution:
 

Question 8.
Solve the inquation 8 – 2x > x – 5 ; x ∈ N.
Solution:
 

x = 1, 2, 3, 4 (x ∈ N)
Solution set = {1, 2, 3, 4}

Question 9.
Solve the inequality 18 – 3 (2x – 5) > 12; x ∈ W.
Solution:
 

Question 10.
Solve :  + 15 < 17; x ∈ W.
Solution:
 

Question 11.
Solve : -3 + x < 2, x ∈ N
Solution:
 

Question 12.
Solve : 4x – 5 > 10 – x, x ∈ {0, 1, 2, 3, 4, 5, 6, 7}
Solution:
 

Solution set = {4, 5, 6, 7}

Question 13.
Solve : 15 – 2(2x – 1) < 15, x ∈ Z.
Solution:
 

Question 14.
Solve :  >  , x ∈ W.
Solution:

 

Linear Inequations Exercise 15B – Selina Concise Mathematics Class 8 ICSE Solutions

Solve and graph the solution set on a number line :
Question 1.
x – 5 < -2 ; x ∈ N
Solution:
 

Question 2.
3x – 1 > 5 ; x ∈ W
Solution:
 
Question 3.
-3x + 12 < -15 ; x ∈ R.
Solution:
 

Question 4.
7 > 3x – 8 ; x ∈ W
Solution:
 

Question 5.
8x – 8 < – 24 ; x ∈ Z
Solution:
 

 

Question 6.
8x – 9 > 35 – 3x ; x ∈ N
Solution:
 

Question 7.
5x + 4 > 8x – 11 ; x ∈ Z
Solution:
 

Question 8.

 + 1 < -3 ; x ∈ R

Solution:
 

 

Question 9.

  > -1 +  ; x ∈ N
Solution:
 

Question 10.
 x + 5 ≤  x + 6 ; x ∈ W
Solution:
 

 

Question 11.

Solve the inequation 5(x – 2) > 4 (x + 3) – 24 and represent its solution on a number line.

Given the replacement set is {-4, -3, -2, -1, 0, 1, 2, 3, 4}.

Solution:
 

Question 12.
Solve   (x – 1) + 4 < 10 and represent its solution on a number line.

Given replacement set is {-8, -6, -4, 3, 6, 8, 12}.
Solution:
 

Question 13.
For each inequation, given below, represent the solution on a number line :
(i)  – 2x ≥  ; x ∈ W
(ii) 3(2x – 1) ≥ 2(2x + 3), x ∈ Z
(iii) 2(4 – 3x) ≤ 4(x – 5), x ∈ W
(iv) 4(3x + 1) > 2(4x – 1), x is a negative integer
(v)  < 3, x ∈ R
(vi) -2(x + 8) ≤ 8, x ∈ R
Solution: