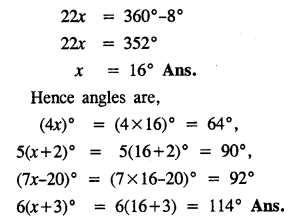Selina Concise Mathematics Class 8 ICSE Solutions Chapter 16 Understanding Shapes

Selina Concise Mathematics Class 8 ICSE Solutions Chapter 16 Understanding Shapes

Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 16 Understanding Shapes (Including Polygons)

Understanding Shapes Exercise 16A – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
State which of the following are polygons :

If the given figure is a polygon, name it as convex or concave.
Solution:
Only Fig. (ii), (iii) and (v) are polygons.
Fig. (ii) and (iii) are concave polygons while
Fig. (v) is convex.

Question 2.
Calculate the sum of angles of a polygon with :
(i) 10 sides
(ii) 12 sides
(iii) 20 sides
(iv) 25 sides
Solution:
(i) No. of sides n = 10
sum of angles of polygon = (n – 2) x 180°
= (10 – 2) x 180° = 1440°
(ii) no. of sides n = 12
sum of angles = (n – 2) x 180°
= (12 – 2) x 180° = 10 x 180° = 1800°
(iii) n = 20
Sum of angles of Polygon = (n – 2) x 180°
= (20 – 2) x 180° = 3240°
(iv) n = 25
Sum of angles of polygon = (n – 2) x 180°
= (25 – 2) x 180° = 4140°

Question 3.
Find the number of sides in a polygon if the sum of its interior angles is :
(i) 900°
(ii) 1620°
(iii) 16 right-angles
(iv) 32 right-angles.
Solution:
(i) Let no. of sides = n
Sum of angles of polygon = 900°
(n – 2) x 180° = 900°
n – 2 = 

n – 2 = 5
n = 5 + 2
n = 7
(ii) Let no. of sides = n
Sum of angles of polygon = 1620°
(n – 2) x 180° = 1620°
n – 2 = 

n – 2 = 9
n = 9 + 2
n = 11
(iii) Let no. of sides = n
Sum of angles of polygon = 16 right angles = 16 x 90 = 1440°
(n – 2) x 180° = 1440°
n – 2 = 
n – 2 = 8
n = 8 + 2
n = 10
(iv) Let no. of sides = n
Sum of angles of polygon = 32 right angles = 32 x 90 = 2880°
(n – 2) x 180° = 2880
n – 2 = 

n – 2 = 16
n = 16 + 2
n = 18

Question 4.
Is it possible to have a polygon ; whose sum of interior angles is :
(i) 870°
(ii) 2340°
(iii) 7 right-angles
(iv) 4500°
Solution:
(i) Let no. of sides = n
Sum of angles = 870°
(n – 2) x 180° = 870°
n – 2 = 
n – 2 = 


n =  + 2
n = 


Which is not a whole number.
Hence it is not possible to have a polygon, the sum of whose interior angles is 870°
(ii) Let no. of sides = n
Sum of angles = 2340°
(n – 2) x 180° = 2340°
n – 2 = 


n – 2 = 13
n = 13 + 2 = 15
Which is a whole number.
Hence it is possible to have a polygon, the sum of whose interior angles is 2340°.
(iii) Let no. of sides = n
Sum of angles = 7 right angles = 7 x 90 = 630°
(n – 2) x 180° = 630°
n – 2 = 


n – 2 = 


n =   + 2

n = 

Which is not a whole number. Hence it is not possible to have a polygon, the sum of whose interior angles is 7 right-angles.

(iv) Let no. of sides = n

(n – 2) x 180° = 4500°
n – 2 = 
n – 2 = 25
n = 25 + 2
n = 27
Which is a whole number.
Hence it is possible to have a polygon, the sum of whose interior angles is 4500°.

Question 5.
(i) If all the angles of a hexagon are equal ; find the measure of each angle.
(ii) If all the angles of a 14-sided figure are equal ; find the measure of each angle.
Solution:
(i) No. of sides of hexagon, n = 6
Let each angle be = x°
Sum of angles = 6x°
(n – 2) x 180° = Sum of angles
(6 – 2) x 180° = 6x°
4 x 180 = 6x

Question 6.

Find the sum of exterior angles obtained on producing, in order, the sides of a polygon with :

(i) 7 sides

(ii) 10 sides
(iii) 250 sides.
Solution:
(i) No. of sides n = 7
Sum of interior & exterior angles at one vertex = 180°

Question 7.

The sides of a hexagon are produced in order. If the measures of exterior angles so obtained are (6x – 1)°, (10x + 2)°, (8x + 2)° (9x – 3)°, (5x + 4)° and (12x + 6)° ; find each exterior angle.

Solution:

Sum of exterior angles of hexagon formed by producing sides of order = 360°

i.e. 41° ; 72°, 58° ; 60° ; 39° and 90°

Question 8.

The interior angles of a pentagon are in the ratio 4 : 5 : 6 : 7 : 5. Find each angle of the pentagon.

Solution:

Let the interior angles of the pentagon be 4x, 5x, 6x, 7x, 5x.
Their sum = 4x + 5x + 6x + 7x + 5x = 21x

Question 9.

Two angles of a hexagon are 120° and 160°. If the remaining four angles are equal, find each equal angle.

Solution:

Two angles of a hexagon are 120°, 160°
Let remaining four angles be x, x, x and x.
Their sum = 4x + 280°
But sum of all the interior angles of a hexagon

Question 10.

The figure, given below, shows a pentagon ABCDE with sides AB and ED parallel to each other, and ∠B : ∠C : ∠D = 5 : 6 : 7.

  

(i) Using formula, find the sum of interior angles of the pentagon.
(ii) Write the value of ∠A + ∠E
(iii) Find angles B, C and D.
Solution:
(i) Sum of interior angles of the pentagon

Question 11.

Two angles of a polygon are right angles and the remaining are 120° each. Find the number of sides in it.

Solution:

Let number of sides = n

n = 


n = 5

Question 12.

In a hexagon ABCDEF, side AB is parallel to side FE and ∠B : ∠C : ∠D : ∠E = 6 : 4 : 2 : 3. Find ∠B and ∠D.

Solution:

Question 13.

the angles of a hexagon are x + 10°, 2x + 20°, 2x – 20°, 3x – 50°, x + 40° and x + 20°. Find x.

Solution:

Question 14.

In a pentagon, two angles are 40° and 60°, and the rest are in the ratio 1 : 3 : 7. Find the biggest angle of the pentagon.

Solution:

In a pentagon, two angles are 40° and 60° Sum of remaining 3 angles = 3 x 180°
= 540° – 40° – 60° = 540° – 100° = 440°
Ratio in these 3 angles =1 : 3 : 7
Sum of ratios =1 + 3 + 7 = 11
Biggest angle =  = 280°

Understanding Shapes Exercise 16B – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Fill in the blanks :
In case of regular polygon, with :

Solution:

Question 2.
Find the number of sides in a regular polygon, if its each interior angle is :
(i) 160°
(ii) 135°
(iii)  of a right-angle
Solution:

Question 3.
Find the number of sides in a regular polygon, if its each exterior angle is :
(i)  of a right angle
(ii) two-fifth of a right-angle.
Solution:

(i) Each exterior angle =   of a right angle

=   x 90

= 30°
Let number of sides = n

Question 4.
Is it possible to have a regular polygon whose each interior angle is :
(i) 170°
(ii) 138°
Solution:
(i) No. of sides = n
each interior angle = 170°

Which is not a whole number.

Hence it is not possible to have a regular polygon having interior angle of 138°.

Question 5.

Is it possible to have a regular polygon whose each exterior angle is :
(i) 80°
(ii) 40% of a right angle.
Solution:
(i) Let no. of sides = n each exterior angle = 80°

Which is not a whole number.

Hence it is not possible to have a regular polygon whose each exterior angle is of 80°.

(ii) Let number of sides = n

Each exterior angle = 40% of a right angle

Which is a whole number.

Hence it is possible to have a regular polygon whose each exterior angle is 40% of a right angle.

Question 6.

Find the number of sides in a regular polygon, if its interior angle is equal to its exterior angle.

Solution:

Let each exterior angle or interior angle be = x°

Question 7.

The exterior angle of a regular polygon is one-third of its interior angle. Find the number of sides in the polygon.

Solution:

Let interior angle = x°
Exterior angle =  x°

Question 8.

The measure of each interior angle of a regular polygon is five times the measure of its exterior angle. Find :

(i) measure of each interior angle ;

(ii) measure of each exterior angle and
(iii) number of sides in the polygon.
Solution:
Let exterior angle = x°
Interior angle = 5x°
x + 5x = 180°
6x = 180°
x = 30°
Each exterior angle = 30°
Each interior angle = 5 x 30° = 150°
Let no. of sides = n

Question 9.

The ratio between the interior angle and the exterior angle of a regular polygon is 2 : 1. Find :

(i) each exterior angle of the polygon ;

(ii) number of sides in the polygon
Solution:
Interior angle : exterior angle = 2 : 1
Let interior angle = 2x° & exterior angle = x°

Question 10.

The ratio between the exterior angle and the interior angle of a regular polygon is 1 : 4. Find the number of sides in the polygon.

Solution:

Let exterior angle = x° & interior angle = 4x°

Question 11.

The sum of interior angles of a regular polygon is twice the sum of its exterior angles. Find the number of sides of the polygon.

Solution:

Let number of sides = n
Sum of exterior angles = 360°
Sum of interior angles = 360° x 2 = 720°
Sum of interior angles = (n – 2) x 180°
720° = (n – 2) x 180°
n – 2 = 

n – 2 = 4
n = 4 + 2
n = 6

Question 12.

AB, BC and CD are three consecutive sides of a regular polygon. If angle BAC = 20° ; find :

(i) its each interior angle,

(ii) its each exterior angle
(iii) the number of sides in the polygon.
Solution:

Question 13.

Two alternate sides of a regular polygon, when produced, meet at the right angle. Calculate the number of sides in the polygon.

Solution:

Question 14.
In a regular pentagon ABCDE, draw a diagonal BE and then find the measure of:
(i) ∠BAE
(ii) ∠ABE
(iii) ∠BED
Solution:
(i) Since number of sides in the pentagon = 5
Each exterior angle =  = 72°
∠BAE = 180° – 72°= 108°

Question 15.
The difference between the exterior angles of two regular polygons, having the sides equal to (n – 1) and (n + 1) is 9°. Find the value of n.
Solution:
We know that sum of exterior angles of a polynomial is 360°
(i) If sides of a regular polygon = n – 1

Question 16.

If the difference between the exterior angle of a n sided regular polygon and an (n + 1) sided regular polygon is 12°, find the value of n.

Solution:

We know that sum of exterior angles of a polygon = 360°
Each exterior angle of a regular polygon of 360°

Question 17.

The ratio between the number of sides of two regular polygons is 3 : 4 and the ratio between the sum of their interior angles is 2 : 3. Find the number of sides in each polygon.

Solution:

Ratio of sides of two regular polygons = 3 : 4
Let sides of first polygon = 3n
and sides of second polygon = 4n
Sum of interior angles of first polygon

Question 18.

Three of the exterior angles of a hexagon are 40°, 51 ° and 86°. If each of the remaining exterior angles is x°, find the value of x.

Solution:

Sum of exterior angles of a hexagon = 4 x 90° = 360°
Three angles are 40°, 51° and 86°
Sum of three angle = 40° + 51° + 86° = 177°
Sum of other three angles = 360° – 177° = 183°
Each angle is x°
3x = 183°
x = 
Hence x = 61

Question 19.
Calculate the number of sides of a regular polygon, if:
(i) its interior angle is five times its exterior angle.
(ii) the ratio between its exterior angle and interior angle is 2 : 7.
(iii) its exterior angle exceeds its interior angle by 60°.
Solution:
Let number of sides of a regular polygon = n
(i) Let exterior angle = x
Then interior angle = 5x
x + 5x = 180°
=> 6x = 180°

Question 20.

The sum of interior angles of a regular polygon is thrice the sum of its exterior angles. Find the number of sides in the polygon.

Solution:

Sum of interior angles = 3 x Sum of exterior angles
Let exterior angle = x
The interior angle = 3x
x + 3x=180°
=> 4x = 180°
=> x = 
=> x = 45°
Number of sides =  = 8

Understanding Shapes Exercise 16C – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.

Two angles of a quadrilateral are 89° and 113°. If the other two angles are equal; find the equal angles.

Solution:

Let the other angle = x°
According to given,
89° + 113° + x° + x° = 360°
2x° = 360° – 202°
2x° = 158°
x° = 
other two angles = 79° each

Question 2.

Two angles of a quadrilateral are 68° and 76°. If the other two angles are in the ratio 5 : 7; find the measure of each of them.

Solution:

Two angles are 68° and 76°
Let other two angles be 5x and 7x
68° + 76°+ 5x + 7x = 360°
12x + 144° = 360°
12x = 360° – 144°
12x = 216°
x = 18°
angles are 5x and 7x
i.e. 5 x 18° and 7 x 18° i.e. 90° and 126°

Question 3.
Angles of a quadrilateral are (4x)°, 5(x+2)°, (7x – 20)° and 6(x+3)°. Find :
(i) the value of x.
(ii) each angle of the quadrilateral.
Solution:
Angles of quadrilateral are,

Question 4.

Use the information given in the following figure to find :
(i) x
(ii) ∠B and ∠C

Solution:

Question 5.

In quadrilateral ABCD, side AB is parallel to side DC. If ∠A : ∠D = 1 : 2 and ∠C : ∠B = 4 : 5

(i) Calculate each angle of the quadrilateral.

(ii) Assign a special name to quadrilateral ABCD
Solution:

Question 6.
From the following figure find ;
(i) x
(ii) ∠ABC
(iii) ∠ACD
Solution:

(i) In Quadrilateral ABCD,
x + 4x + 3x + 4x + 48° = 360°
12x = 360° – 48°
12x = 312

Question 7.

Given : In quadrilateral ABCD ; ∠C = 64°, ∠D = ∠C – 8° ; ∠A = 5(a+2)° and ∠B = 2(2a+7)°.

Calculate ∠A.

Solution:
∠C = 64° (Given)
∠D = ∠C – 8° = 64°- 8° = 56°
∠A = 5(a+2)°
∠B = 2(2a+7)°
Now ∠A + ∠B + ∠C + ∠D = 360°
5(a+2)° + 2(2a+7)° + 64° + 56° = 360°
5a + 10 + 4a + 14° + 64° + 56° = 360°
9a + 144° = 360°
9a = 360° – 144°
9a = 216°
a = 24°
∠A = 5 (a + 2) = 5(24+2) = 130°

Question 8.
In the given figure : ∠b = 2a + 15 and ∠c = 3a + 5; find the values of b and c.

Solution:
Stun of angles of quadrilateral = 360°
70° + a + 2a + 15 + 3a + 5 = 360°
6a + 90° = 360°
6a = 270°
a = 45°
b = 2a + 15 = 2 x 45 + 15 = 105°
c = 3a + 5 = 3 x 45 + 5 = 140°
Hence ∠b and ∠c are 105° and 140°

Question 9.

Three angles of a quadrilateral are equal. If the fourth angle is 69°; find the measure of equal angles.

Solution:

Let each equal angle be x°
x + x + x + 69° = 360°

3x = 360°- 69
3x = 291
x = 97°
Each, equal angle = 97°

Question 10.
In quadrilateral PQRS, ∠P : ∠Q : ∠R : ∠S = 3 : 4 : 6 : 7.

Calculate each angle of the quadrilateral and then prove that PQ and SR are parallel to each other

(i) Is PS also parallel to QR ?

(ii) Assign a special name to quadrilateral PQRS.
Solution:

Question 11.
Use the informations given in the following figure to find the value of x.

Solution:
Take A, B, C, D as the vertices of Quadrilateral and BA is produced to E (say).
Since ∠EAD = 70°
∠DAB = 180° – 70°= 110°
[EAB is a straight line and AD stands on it ∠EAD+ ∠DAB = 180°]
110° + 80° + 56° + 3x – 6° = 360°
[sum of interior angles of a quadrilateral = 360°]
3x = 360° – 110° – 80° – 56° + 6°
3x = 360° – 240° = 120°
x = 40°

Question 12.

The following figure shows a quadrilateral in which sides AB and DC are parallel. If ∠A : ∠D = 4 : 5, ∠B = (3x – 15)° and ∠C = (4x + 20)°, find each angle of the quadrilateral ABCD.

  

Solution:
Let ∠A = 4x
∠D = 5x
Since ∠A + ∠D = 180° [AB||DC]
4x + 5x = 180°
=> 9x = 180°
=> x = 20°
∠A = 4 (20) = 80°,
∠D = 5 (20) = 100°
Again ∠B + ∠C = 180° [ AB||DC]
3x – 15° + 4x + 20° = 180°
7x = 180° – 5°
=> 7x = 175°
=> x = 25°
∠B = 75° – 15° = 60°
and ∠C = 4 (25) + 20 = 100°+ 20°= 120°

Question 13.
Use the following figure to find the value of x

Solution:
The sum of exterior angles of a quadrilateral

=> y + 80° + 60° + 90° = 360°
=> y + 230° = 360°
=> y = 360° – 230° = 130°
At vertex A,
∠y + ∠x = 180° (Linear pair)
x = 180° – 130°
=> x = 50°

Question 14.

ABCDE is a regular pentagon. The bisector of angle A of the pentagon meets the side CD in point M. Show that ∠AMC = 90°.

Solution:

Given : ABCDE is a regular pentagon.
The bisector ∠A of the pentagon meets the side CD at point M.
To prove : ∠AMC = 90°

Proof: We know that, the measure of each interior angle of a regular pentagon is 108°.

∠BAM =  x 108° = 54°

Since, we know that the sum of a quadrilateral is 360°
In quadrilateral ABCM, we have
∠BAM + ∠ABC + ∠BCM + ∠AMC = 360°
54° + 108° + 108° + ∠AMC = 360°
∠AMC = 360° – 270°
∠AMC = 90°

Question 15.

In a quadrilateral ABCD, AO and BO are bisectors of angle A and angle B respectively. Show that:

∠AOB =  (∠C + ∠D)

Solution:
Given : AO and BO are the bisectors of ∠A and ∠B respectively.
∠1 = ∠4 and ∠3 = ∠5 ……..(i)

To prove : ∠AOB = (∠C + ∠D)
Proof: In quadrilateral ABCD
∠A + ∠B + ∠C + ∠D = 360°
 (∠A + ∠B + ∠C + ∠D) = 180° …………(ii)
Now in ∆AOB
∠1 + ∠2 + ∠3 = 180° ………(iii)
Equating equation (ii) and equation (iii), we get
∠1 + ∠2 + ∠3 = ∠A + ∠B +   (∠C + ∠D)

∠1 + ∠2 + ∠3 = ∠1 + ∠3 +   (∠C + ∠D)

∠2 =   (∠C + ∠D)

∠AOB =   (∠C + ∠D)

Hence proved.