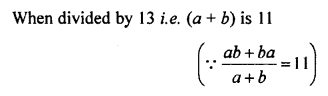Selina Concise Mathematics Class 8 ICSE Solutions Chapter 5 Playing with Number

Selina Concise Mathematics Class 8 ICSE Solutions Chapter 5 Playing with Number

Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 5 Playing with Number

Playing with Number Exercise 5A – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Write the quotient when the sum of 73 and 37 is divided by
(i) 11
(ii) 10
Solution:

Question 2.
Write the quotient when the sum of 94 and 49 is divided by
(i) 11
(ii) 13
Solution:

Question 3.
Find the quotient when 73 – 37 is divided by
(i) 9
(ii) 4
Solution:

Question 4.
Find the quotient when 94 – 49 is divided by
(i) 9
(ii) 5
Solution:

Question 5.
Show that 527 + 752 + 275 is exactly divisible by 14.
Solution:
Property :
abc = 100a + 106 + c ………(i)
bca = 1006 + 10c + a ……..(ii)
and cab = 100c + 10a + b ……….(iii)

Adding, (i), (ii) and (iii), we get abc + bca + cab = 111a + 111b + 111c = 111(a + b + c) = 3 x 37(a + b + c)

Now, let us try this method on

527 + 752 + 275 to check is it exactly divisible by 14
Here, a = 5, 6 = 2, c = 7
527 + 752 + 275 = 3 x 37(5 + 2 + 7) = 3 x 37 x 14
Hence, it shows that 527 + 752 + 275 is exactly divisible by 14

Question 6.
If a = 6, show that abc = bac.
Solution:
Given : a = 6
To show : abc = bac
Proof: abc = 100a + 106 + c …….(i)
(By using property 3)
bac = 1006 + 10a + c —(ii)
(By using property 3)
Since, a = 6
Substitute the value of a = 6 in equation (i) and (ii), we get
abc = 1006 + 106 + c ………(iii)
bac = 1006 + 106 + c ………(iv)
Subtracting (iv) from (iii) abc – bac = 0
abc = bac
Hence proved.

Question 7.
If a > c; show that abc – cba = 99(a – c).
Solution:
Given, a > c
To show : abc – cba = 99(a – c)
Proof: abc = 100a + 10b + c ……….(i)
(By using property 3)
cba = 100c + 10b + a ………..(ii)
(By using property 3)
Subtracting, equation (ii) from (i), we get
abc – cba = 100a + c – 100c – a
abc – cba = 99a – 99c
abc – cba = 99(a – c)
Hence proved.

Question 8.
If c > a; show that cba – abc = 99(c – a).
Solution:
Given : c > a
To show : cba – abc = 99(c – a)
Proof:
cba = 100c + 106 + a ……….(i)
(By using property 3)
abc = 100a + 106 + c ………(ii)
(By using property 3)
Subtracting (ii) from (i)
cba – abc= 100c+ 106 + a- 100a- 106-c
=> cba – abc = 99c – 99a
=> cba – abc = 99(c – a)
Hence proved.

Question 9.
If a = c, show that cba – abc = 0.
Solution:
Given : a = c
To show : cba – abc = 0
Proof:
cba = 100c + 106 + a …………(i)
(By using property 3)
abc = 100a + 106 + c …………(ii)
(By using property 3)
Since, a = c,
Substitute the value of a = c in equation (i) and (ii), we get
cba = 100c + 10b + c ……….(iii)
abc = 100c + 10b + c …………(iv)
Subtracting (iv) from (iii), we get
cba – abc – 100c + 106 + c – 100c – 106 – c
=> cba – abc = 0
=> cba = abc
Hence proved.

Question 10.
Show that 954 – 459 is exactly divisible by 99.
Solution:
To show : 954 – 459 is exactly divisible by 3 99, where a = 9, b = 5, c = 4
abc = 100a + 10b + c
=> 954 = 100 x 9 + 10 x 5 + 4
=> 954 = 900 + 50 + 4 ………(i)
and 459 = 100 x 4+ 10 x 5 + 9
=> 459 = 400 + 50 + 9 ……..(ii)
Subtracting (ii) from (i), we get
954 – 459 = 900 + 50 + 4 – 400 – 50 – 9
=> 954 – 459 = 500 – 5
=> 954 – 459 = 495
=> 954 – 459 = 99 x 5
Hence, 954 – 459 is exactly divisible by 99
Hence proved.

Playing with Number Exercise 5B – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:
As we need A at unit place and 9 at ten’s place,
A = 6 as 6 x 6 = 36

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:
As we need B at unit place and A at ten’s place,
B = 0 as 5 x 0 = 0
Now we want to find A, 5 x A = A (at unit’s place)
A = 5, as 5 x 5 = 25
C = 2

Question 10.

Solution:

Question 11.

Solution:

Playing with Number Exercise 5C – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Find which of the following nutpbers are divisible by 2:
(i) 192
(ii) 1660
(iii) 1101
(iv) 2079
Solution:
A number having its unit digit 2,4,6,8 or 0 is divisible by 2,
So, Number 192, 1660 are divisible by 2.

Question 2.
Find which of the following numbers are divisible by 3:
(i) 261
(ii) 111
(iii) 6657
(iv) 2574
Solution:
A number is divisible by 3 if the sum of its digits is divisible by 3,
So, 261, 111 are divisible by 3.

Question 3.
Find which of the following numbers are divisible by 4:
(i) 360
(ii) 3180
(iii) 5348
(iv) 7756
Solution:

A number is divisible by 4, if the number formed by the last two digits is divisible by 4.

So, Number 360, 5348, 7756 are divisible by 4.

Question 4.
Find which of the following numbers are divisible by 5 :
(i) 3250
(ii) 5557
(iii) 39255
(iv) 8204
Solution:
A number having its unit digit 5 or 0, is divisible by 5.
So, 3250, 39255 are all divisible by 5.

Question 5.
Find which of the following numbers are divisible by 10:
(i) 5100
(ii) 4612
(iii) 3400
(iv) 8399
Solution:
A number having its unit digit 0, is divisible by 10.
So, 5100, 3400 are all divisible by 10.

Question 6.
Which of the following numbers are divisible by 11 :
(i) 2563
(ii) 8307
(iii) 95635
Solution:

A number is divisible by 11 if the difference of the sum of digits at the odd places and sum of the digits at even places is zero or divisible by 11.

So, 2563 is divisible by 11.

Playing with Number Exercise 5D – Selina Concise Mathematics Class 8 ICSE Solutions

For what value of digit x, is :

Question 1.
1×5 divisible by 3 ?
Solution:
1×5 is divisible by 3
=> 1 + x + 5 is a multiple of 3
=> 6 + x = 0, 3, 6, 9,
=> x = -6, -3, 0, 3, 6, 9
Since, x is a digit
x = 0, 3, 6 or 9

Question 2.
31×5 divisible by 3 ?
Solution:
31×5 is divisible by 3
=> 3 + 1 + x + 5 is a multiple of 3
=> 9 + x = 0, 3, 6, 9,
=> x = -9, -6, -3, 0, 3, 6, 9,
Since, x is a digit
x = 0, 3, 6 or 9

Question 3.
28×6 a multiple of 3 ?
Solution:
28×6 is a multiple of 3
2 + 8+ x + 6 is a multiple of 3
=> 16 + x = 0, 3, 6, 9, 12, 15, 18
=> x = -18, -5, -2, 0, 2, 5, 8
Since, x is a digit = 2, 5, 8

Question 4.
24x divisible by 6 ?
Solution:
24x is divisible by 6
=> 2 + 4+ x is a multiple of 6
=> 6 + x = 0, 6, 12
=> x = -6, 0, 6
Since, x is a digit
x = 0, 6

Question 5.
3×26 a multiple of 6 ?
Solution:
3×26 is a multiple of 6
3 + x + 2 + 6 is a multiple of 3
=> 11 + x = 0, 3, 6, 9, 12, 15, 18,21,
=> x = -11, -8, -5, -2, 1, 4, 7, 10, ….
Since, x is a digit
x = 1, 4 or 7

Question 6.
42×8 divisible by 4 ?
Solution:
42×8 is divisible by 4
=> 4 + 2 + x + 8 is a multiple of 2
=> 14 + x = 0, 2, 4, 6, 8,
=> x = -8, -6, -4, -2, 2, 4, 6, 8,
Since, x is a digit 2, 4, 6, 8

Question 7.
9142x a multiple of 4 ?
Solution:
9142x is multiple of 4
=> 9 + 1 + 4 + 2 + x is a multiple of 4
=> 16 + x = 0, 4, 8, ………
x = -8, -4, 0, 4, 8
Since, x is a digit
4, 8

Question 8.
7×34 divisible by 9 ?
Solution:
7×34 is multiple of 9
=> 7 + x + 3+ 4 is a multiple of 9
=> 14 + x = 0, 9, 18, 27,
=> x = -1, 4, 13,
Since, x is a digit
x = 4

Question 9.
5×555 a multiple of 9 ?
Solution:
Sum of the digits of 5×555
=5 + x + 5 + 5 + 5 = 20 + x
It is multiple by 9
The sum should be divisible by 9
Value of x will be 7

Question 10.
3×2 divisible by 11 ?
Solution:
Sum of the digit in even place = x
and sum of the digits in odd place = 3 + 2 = 5

Difference of the sum of the digits in even places and in odd places = x – 5

3×2 is a multiple of 11

=> x – 5 = 0, 11, 22,
=> x = 5, 16, 27,
Since, x is a digit x = 5

Question 11.
5×2 a multiple of 11 ?
Solution:
Sum of a digit in even place = x
and sum of the digits in odd place = 5 + 2 = 7

Difference of the sum of the digits in even places and in odd places = x – 7

5×2 is a multiple of 11

=> x – 7 = 0, 11, 22,
=> x = 7, 18, 29,
Since, x is a digit
x = 7