Selina Concise Mathematics Class 10 ICSE Solutions Reflection
Selina Publishers Concise Mathematics Class 10 ICSE Solutions Chapter 12 Reflection (In x-axis, y-axis, x=a, y=a and the origin ; Invariant Points)
Reflection Exercise 12A – Selina Concise Mathematics Class 10 ICSE Solutions
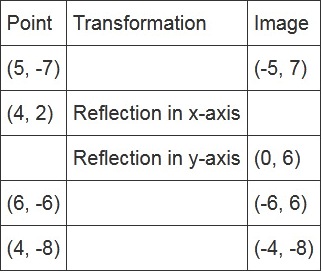
Question 1.
Complete the following table:
Solution:
Question 2.
A point P is its own image under the reflection in a line l. Describe the position of point the P with respect to the line l.
Solution:
Since, the point P is its own image under the reflection in the line l. So, point P is an invariant point.
Hence, the position of point P remains unaltered.
Question 3.
State the co-ordinates of the following points under reflection in x-axis:
(i) (3, 2)
(ii) (-5, 4)
(iii) (0, 0)
Solution:
(i) (3, 2)
The co-ordinate of the given point under reflection in the x-axis is (3, -2).
(ii) (-5, 4)
The co-ordinate of the given point under reflection in the x-axis is (-5, -4).
(iii) (0, 0)
The co-ordinate of the given point under reflection in the x-axis is (0, 0).
Question 4.
State the co-ordinates of the following points under reflection in y-axis:
(i) (6, -3)
(ii) (-1, 0)
(iii) (-8, -2)
Solution:
(i) (6, -3)
The co-ordinate of the given point under reflection in the y-axis is (-6, -3).
(ii) (-1, 0)
The co-ordinate of the given point under reflection in the y-axis is (1, 0).
(iii) (-8, -2)
The co-ordinate of the given point under reflection in the y-axis is (8, -2).
Question 5.
State the co-ordinates of the following points under reflection in origin:
(i) (-2, -4)
(ii) (-2, 7)
(iii) (0, 0)
Solution:
(i) (-2, -4)
The co-ordinate of the given point under reflection in origin is (2, 4).
(ii) (-2, 7)
The co-ordinate of the given point under reflection in origin is (2, -7).
(iii) (0, 0)
The co-ordinate of the given point under reflection in origin is (0, 0).
Question 6.
State the co-ordinates of the following points under reflection in the line x = 0:
(i) (-6, 4)
(ii) (0, 5)
(iii) (3, -4)
Solution:
(i) (-6, 4)
The co-ordinate of the given point under reflection in the line x = 0 is (6, 4).
(ii) (0, 5)
The co-ordinate of the given point under reflection in the line x = 0 is (0, 5).
(iii) (3, -4)
The co-ordinate of the given point under reflection in the line x = 0 is (-3, -4).
Question 7.
State the co-ordinates of the following points under reflection in the line y = 0:
(i) (-3, 0)
(ii) (8, -5)
(iii) (-1, -3)
Solution:
(i) (-3, 0)
The co-ordinate of the given point under reflection in the line y = 0 is (-3, 0).
(ii) (8, -5)
The co-ordinate of the given point under reflection in the line y = 0 is (8, 5).
(iii) (-1, -3)
The co-ordinate of the given point under reflection in the line y = 0 is (-1, 3).
Question 8.
A point P is reflected in the x-axis. Co-ordinates of its image are (-4, 5).
(i) Find the co-ordinates of P.
(ii) Find the co-ordinates of the image of P under reflection in the y-axis.
Solution:
(i) Since, Mx (-4, -5) = (-4, 5)
So, the co-ordinates of P are (-4, -5).
(ii) Co-ordinates of the image of P under reflection in the y-axis (4, -5).
Question 9.
A point P is reflected in the origin. Co-ordinates of its image are (-2, 7).
(i) Find the co-ordinates of P.
(ii) Find the co-ordinates of the image of P under reflection in the x-axis.
Solution:
(i) Since, MO (2, -7) = (-2, 7)
So, the co-ordinates of P are (2, -7).
(ii) Co-ordinates of the image of P under reflection in the x-axis (2, 7).
Question 10.
The point (a, b) is first reflected in the origin and then reflected in the y-axis to P’. If P’ has co-ordinates (4, 6); evaluate a and b.
Solution:
MO (a, b) = (-a, -b)
My (-a, -b) = (a, -b)
Thus, we get the co-ordinates of the point P’ as (a, -b). It is given that the co-ordinates of P’ are (4, 6).
On comparing the two points, we get, a = 4 and b = -6
Question 11.
The point P (x, y) is first reflected in the x-axis and reflected in the origin to P’. If P’ has co-ordinates (-8, 5); evaluate x and y.
Solution:
Mx (x, y) = (x, -y)
MO (x, -y) = (-x, y)
Thus, we get the co-ordinates of the point P’ as (-x, y). It is given that the co-ordinates of P’ are (-8, 5).
On comparing the two points, we get, x = 8 and y = 5
Question 12.
The point A (-3, 2) is reflected in the x-axis to the point A’. Point A’ is then reflected in the origin to point A”.
(i) Write down the co-ordinates of A”.
(ii) Write down a single transformation that maps A onto A”.
Solution:
(i) The reflection in x-axis is given by Mx (x, y) = (x, -y).
A’ = reflection of A (-3, 2) in the x- axis = (-3, -2).
The reflection in origin is given by MO (x, y) = (-x, -y).
A” = reflection of A’ (-3, -2) in the origin = (3, 2)
(ii) The reflection in y-axis is given by My (x, y) = (-x, y).
The reflection of A (-3, 2) in y-axis is (3, 2).
Thus, the required single transformation is the reflection of A in the y-axis to the point A”.
Question 13.
The point A (4, 6) is first reflected in the origin to point A’. Point A’ is then reflected in the y-axis to the point A”.
(i) Write down the co-ordinates of A”.
(ii) Write down a single transformation that maps A onto A”.
Solution:
(i) The reflection in origin is given by MO (x, y) = (-x, -y).
A’ = reflection of A (4, 6) in the origin = (-4, -6)
The reflection in y-axis is given by My (x, y) = (-x, y).
A” = reflection of A’ (-4, -6) in the y-axis = (4, -6)
(ii) The reflection in x-axis is given by Mx (x, y) = (x, -y).
The reflection of A (4, 6) in x-axis is (4, -6).
Thus, the required single transformation is the reflection of A in the x-axis to the point A”.
Question 14.
The triangle ABC, where A is (2, 6), B is (-3, 5) and C is (4, 7), is reflected in the y-axis to triangle A’B’C’. Triangle A’B’C’ is then reflected in the origin to triangle A”B”C”.
(i) Write down the co-ordinates of A”, B” and C”.
(ii) Write down a single transformation that maps triangle ABC onto triangle A”B”C”.
Solution:
(i) Reflection in y-axis is given by My (x, y) = (-x, y)
∴ A’ = Reflection of A (2, 6) in y-axis = (-2, 6)
Similarly, B’ = (3, 5) and C’ = (-4, 7)
Reflection in origin is given by MO (x, y) = (-x, -y)
∴ A” = Reflection of A’ (-2, 6) in origin = (2, -6)
Similarly, B” = (-3, -5) and C” = (4, -7)
(ii) A single transformation which maps triangle ABC to triangle A”B”C” is reflection in x-axis.
Question 15.
P and Q have co-ordinates (-2, 3) and (5, 4) respectively. Reflect P in the x-axis to P’ and Q in the y-axis to Q’. State the co-ordinates of P’ and Q’.
Solution:
Reflection in x-axis is given by Mx (x, y) = (x, -y)
P’ = Reflection of P(-2, 3) in x-axis = (-2, -3)
Reflection in y-axis is given by My (x, y) = (-x, y)
Q’ = Reflection of Q(5, 4) in y-axis = (-5, 4)
Thus, the co-ordinates of points P’ and Q’ are (-2, -3) and (-5, 4) respectively.
Question 16.
On a graph paper, plot the triangle ABC, whose vertices are at points A (3, 1), B (5, 0) and C (7, 4).
On the same diagram, draw the image of the triangle ABC under reflection in the origin O (0, 0).
Solution:
The graph shows triangle ABC and triangle A’B’C’ which is obtained when ABC is reflected in the origin.
Question 17.
Find the image of point (4, -6) under the following operations:
(i) Mx . My (ii) My . Mx
(iii) MO . Mx (iv) Mx . MO
(v) MO . My (vi) My . MO
Write down a single transformation equivalent to each operation given above. State whether:
(a) MO . Mx = Mx . MO
(b) My . MO = MO . My
Solution:
(i) Mx . My (4, -6) = Mx (-4, -6) = (-4, 6)
Single transformation equivalent to Mx . My is MO.
(ii) My . Mx (4, -6) = My (4, 6) = (-4, 6)
Single transformation equivalent to My . Mx is MO.
(iii) MO . Mx (4, -6) = MO (4, 6) = (-4, -6)
Single transformation equivalent to MO . Mx is My.
(iv) Mx . MO (4, -6) = Mx (-4, 6) = (-4, -6)
Single transformation equivalent to Mx . MO is My.
(v) MO . My (4, -6) = MO (-4, -6) = (4, 6)
Single transformation equivalent to MO . My is Mx.
(vi) My . MO (4, -6) = My (-4, 6) = (4, 6)
Single transformation equivalent to Mx . MO is Mx.
From (iii) and (iv), it is clear that MO . Mx = Mx . MO.
From (v) and (vi), it is clear that My . MO = MO . My.
Question 18.
Point A (4, -1) is reflected as A’ in the y-axis. Point B on reflection in the x-axis is mapped as B’ (-2, 5). Write down the co-ordinates of A’ and B.
Solution:
Reflection in y-axis is given by My (x, y) = (-x, y)
A’ = Reflection of A(4, -1) in y-axis = (-4, -1)
Reflection in x-axis is given by Mx (x, y) = (x, -y)
B’ = Reflection of B in x-axis = (-2, 5)
Thus, B = (-2, -5)
Question 19.
The point (-5, 0) on reflection in a line is mapped as (5, 0) and the point (-2, -6) on reflection in the same line is mapped as (2, -6).
(a) Name the line of reflection.
(b) Write down the co-ordinates of the image of (5, -8) in the line obtained in (a).
Solution:
(a) We know that reflection in the line x = 0 is the reflection in the y-axis.
It is given that:
Point (-5, 0) on reflection in a line is mapped as (5, 0).
Point (-2, -6) on reflection in the same line is mapped as (2, -6).
Hence, the line of reflection is x = 0.
(b) It is known that My (x, y) = (-x, y)
Co-ordinates of the image of (5, -8) in the line x = 0 are (-5, -8).
Reflection Exercise 12B – Selina Concise Mathematics Class 10 ICSE Solutions
Question 1.
Attempt this question on graph paper.
(a) Plot A (3, 2) and B (5, 4) on graph paper. Take 2 cm = 1 unit on both the axes.
(b) Reflect A and B in the x-axis to A’ and B’ respectively. Plot these points also on the same graph paper.
(c) Write down:
(i) the geometrical name of the figure ABB’A’;
(ii) the measure of angle ABB’;
(iii) the image of A” of A, when A is reflected in the origin.
(iv) the single transformation that maps A’ to A”.
Solution:
(c)
(i) From graph, it is clear that ABB’A’ is an isosceles trapezium.
(ii) The measure of angle ABB’ is 45°.
(iii) A” = (-3, -2)
(iv) Single transformation that maps A’ to A” is the reflection in y-axis.
Question 2.
Points (3, 0) and (-1, 0) are invariant points under reflection in the line L1; points (0, -3) and (0, 1) are invariant points on reflection in line L2.
(i) Name or write equations for the lines L1 and L2.
(ii) Write down the images of the points P (3, 4) and Q (-5, -2) on reflection in line L1. Name the images as P’ and Q’ respectively.
(iii) Write down the images of P and Q on reflection in L2. Name the images as P” and Q” respectively.
(iv) State or describe a single transformation that maps P’ onto P”.
Solution:
(i) We know that every point in a line is invariant under the reflection in the same line.
Since points (3, 0) and (-1, 0) lie on the x-axis.
So, (3, 0) and (-1, 0) are invariant under reflection in x-axis.
Hence, the equation of line L1 is y = 0.
Similarly, (0, -3) and (0, 1) are invariant under reflection in y-axis.
Hence, the equation of line L2 is x = 0.
(ii) P’ = Image of P (3, 4) in L1 = (3, -4)
Q’ = Image of Q (-5, -2) in L1 = (-5, 2)
(iii) P” = Image of P (3, 4) in L2 = (-3, 4)
Q” = Image of Q (-5, -2) in L2 = (5, -2)
(iv) Single transformation that maps P’ onto P” is reflection in origin.
Question 3.
(i) Point P (a, b) is reflected in the x-axis to P’ (5, -2). Write down the values of a and b.
(ii) P” is the image of P when reflected in the y-axis. Write down the co-ordinates of P”.
(iii) Name a single transformation that maps P’ to P”.
Solution:
(i) We know Mx (x, y) = (x, -y)
P’ (5, -2) = reflection of P (a, b) in x-axis.
Thus, the co-ordinates of P are (5, 2).
Hence, a = 5 and b = 2.
(ii) P” = image of P (5, 2) reflected in y-axis = (-5, 2)
(iii) Single transformation that maps P’ to P” is the reflection in origin.
Question 4.
The point (-2, 0) on reflection in a line is mapped to (2, 0) and the point (5, -6) on reflection in the same line is mapped to (-5, -6).
(i) State the name of the mirror line and write its equation.
(ii) State the co-ordinates of the image of (-8, -5) in the mirror line.
Solution:
(i) We know reflection of a point (x, y) in y-axis is (-x, y).
Hence, the point (-2, 0) when reflected in y-axis is mapped to (2, 0).
Thus, the mirror line is the y-axis and its equation is x = 0.
(ii) Co-ordinates of the image of (-8, -5) in the mirror line (i.e., y-axis) are (8, -5).
Question 5.
The points P (4, 1) and Q (-2, 4) are reflected in line y = 3. Find the co-ordinates of P’, the image of P and Q’, the image of Q.
Solution:
The line y = 3 is a line parallel to x-axis and at a distance of 3 units from it.
Mark points P (4, 1) and Q (-2, 4).
From P, draw a straight line perpendicular to line CD and produce. On this line mark a point P’ which is at the same distance above CD as P is below it.
The co-ordinates of P’ are (4, 5).
Similarly, from Q, draw a line perpendicular to CD and mark point Q’ which is at the same distance below CD as Q is above it.
The co-ordinates of Q’ are (-2, 2).
Question 6.
A point P (-2, 3) is reflected in line x = 2 to point P’. Find the coordinates of P’.
Solution:
The line x = 2 is a line parallel to y-axis and at a distance of 2 units from it.
Mark point P (-2, 3).
From P, draw a straight line perpendicular to line CD and produce. On this line mark a point P’ which is at the same distance to the right of CD as P is to the left of it.
The co-ordinates of P’ are (6, 3).
Question 7.
A point P (a, b) is reflected in the x-axis to P’ (2, -3). Write down the values of a and b. P” is the image of P, reflected in the y-axis. Write down the co-ordinates of P”. Find the co-ordinates of P”’, when P is reflected in the line, parallel to y-axis, such that x = 4.
Solution:
A point P (a, b) is reflected in the x-axis to P’ (2, -3).
We know Mx (x, y) = (x, -y)
Thus, co-ordinates of P are (2, 3). Hence, a = 2 and b = 3.
P” = Image of P reflected in the y-axis = (-2, 3)
P”’ = Reflection of P in the line (x = 4) = (6, 3)
Question 8.
Points A and B have co-ordinates (3, 4) and (0, 2) respectively. Find the image:
(a) A’ of A under reflection in the x-axis.
(b) B’ of B under reflection in the line AA’.
(c) A” of A under reflection in the y-axis.
(d) B” of B under reflection in the line AA”.
Solution:
(a) A’ = Image of A under reflection in the x-axis = (3, -4)
(b) B’ = Image of B under reflection in the line AA’ = (6, 2)
(c) A” = Image of A under reflection in the y-axis = (-3, 4)
(d) B” = Image of B under reflection in the line AA” = (0, 6)
Question 9.
(i) Plot the points A (3, 5) and B (-2, -4). Use 1 cm = 1 unit on both the axes.
(ii) A’ is the image of A when reflected in the x-axis. Write down the co-ordinates of A’ and plot it on the graph paper.
(iii) B’ is the image of B when reflected in the y-axis, followed by reflection in the origin. Write down the co-ordinates of B’ and plot it on the graph paper.
(iv) Write down the geometrical name of the figure AA’BB’.
(v) Name the invariant points under reflection in the x-axis.
Solution:
(i) The points A (3, 5) and B (-2, -4) can be plotted on a graph as shown.
(ii) A’ = Image of A when reflected in the x-axis = (3, -5)
(iii) C = Image of B when reflected in the y-axis = (2, -4)
B’ = Image when C is reflected in the origin = (-2, 4)
(iv) Isosceles trapezium
(v) Any point that remains unaltered under a given transformation is called an invariant.
Thus, the required two points are (3, 0) and (-2, 0).
Question 10.
The point P (5, 3) was reflected in the origin to get the image P’.
(a) Write down the co-ordinates of P’.
(b) If M is the foot if the perpendicular from P to the x-axis, find the co-ordinates of M.
(c) If N is the foot if the perpendicular from P’ to the x-axis, find the co-ordinates of N.
(d) Name the figure PMP’N.
(e) Find the area of the figure PMP’N.
Solution:
(a) Co-ordinates of P’ = (-5, -3)
(b) Co-ordinates of M = (5, 0)
(c) Co-ordinates of N = (-5, 0)
(d) PMP’N is a parallelogram.
(e) Are of PMP’N = 2 (Area of D PMN)
= 2 × ½ × 10 × 3
= 30 sq. units
Question 11.
The point P (3, 4) is reflected to P’ in the x-axis; and O’ is the image of O (the origin) when reflected in the line PP’. Write:
(i) the co-ordinates of P’ and O’.
(ii) the length of the segments PP’ and OO’.
(iii) the perimeter of the quadrilateral POP’O’.
(iv) the geometrical name of the figure POP’O’.
Solution:
(i) Co-ordinates of P’ and O’ are (3, -4) and (6, 0) respectively.
(ii) PP’ = 8 units and OO’ = 6 units.
(iii) From the graph it is clear that all sides of the quadrilateral POP’O’ are equal.
In right Δ PO’Q,
PO’ = √(4)2 + (3)2 = 5 units
So, perimeter of quadrilateral POP’O’ = 4 PO’ = 4 × 5 units = 20 units
(iv) Quadrilateral POP’O’ is a rhombus.
Question 12.
A (1, 1), B (5, 1), C (4, 2) and D (2, 2) are vertices of a quadrilateral. Name the quadrilateral ABCD. A, B, C, and D are reflected in the origin on to A’, B’, C’ and D’ respectively. Locate A’, B’, C’ and D’ on the graph sheet and write their co-ordinates. Are D, A, A’ and D’ collinear?
Solution:
Quadrilateral ABCD is an isosceles trapezium.
Co-ordinates of A’, B’, C’ and D’ are A'(-1, -1), B'(-5, -1), C'(-4, -2) and D'(-2, -2) respectively.
It is clear from the graph that D, A, A’ and D’ are collinear.
Question 13.
P and Q have co-ordinates (0, 5) and (-2, 4).
(a) P is invariant when reflected in an axis. Name the axis.
(b) Find the image of Q on reflection in the axis found in (i).
(c) (0, k) on reflection in the origin is invariant. Write the value of k.
(d) Write the co-ordinates of the image of Q, obtained by reflecting it in the origin followed by reflection in x-axis.
Solution:
(a) Any point that remains unaltered under a given transformation is called an invariant.
It is given that P (0, 5) is invariant when reflected in an axis. Clearly, when P is reflected in the y-axis then it will remain invariant. Thus, the required axis is the y-axis.
(b) The co-ordinates of the image of Q (-2, 4) when reflected in y-axis is (2, 4).
(c) (0, k) on reflection in the origin is invariant. We know the reflection of origin in origin is invariant. Thus, k = 0.
(d) Co-ordinates of image of Q (-2, 4) when reflected in origin = (2, -4)
Co-ordinates of image of (2, -4) when reflected in x-axis = (2, 4)
Thus, the co-ordinates of the point are (2, 4).
Question PQ.
The points P (1, 2), Q (3, 4) and R (6, 1) are the vertices of PQR.
(a) Write down the co-ordinates of P’, Q’ and R’, if P’Q’R’ is the image of PQR, when reflected in the origin.
(b) Write down the co-ordinates of P”, Q” and R”, if P”Q”R” is the image of PQR, when reflected in the x-axis.
(c) Mention the special name of the quadrilateral QRR”Q” and find its area.
Solution:
(a) The co-ordinates of P’, Q’ and R’ are (-1, -2), (-3, -4) and (-6, -1) respectively.
(b) The co-ordinates of P”, Q” and R” are (1, -2), (3, -4) and (6, -1) respectively.
(c) The quadrilateral QRR”Q” is an isosceles trapezium.
Area of QRR”Q” = ½ (RR”+ QQ”) × Height
= ½ (2 + 8) × 3 = 15 sq units
Question 14.
(i) The point P (2, -4) is reflected about the line x = 0 to get the image Q. Find the co-ordinates of Q.
(ii) The point Q is reflected about the line y = 0 to get the image R. Find the co-ordinates or R.
(iii) Name the figure PQR.
(iv) Find the area of figure PQR.
Solution:
Question PQ.
A’ and B’ are images of A (-3, 5) and B (-5, 3) respectively on reflection in y-axis. Find:
(a) the co-ordinates of A’ and B’.
(b) Assign special name of quadrilateral AA’B’B.
(c) Are AB’ and BA’ equal in length?
Solution:
(a) The co-ordinates of A’ and B’ are (3, 5) and (5, 3).
(b) Quadrilateral AA’B’B is an isosceles trapezium.
(c) Yes, AB’ and BA’ are equal in length.
Question 15.
Using a graph paper, plot the point A (6, 4) and B (0, 4).
(a) Reflect A and B in the origin to get the image A’ and B’.
(b) Write the co-ordinates of A’ and B’.
(c) Sate the geometrical name for the figure ABA’B’.
(d) Find its perimeter.
Solution:
Question 16.
Use graph paper for this question. (Take 2 cm = 1 unit along both x and y axis. Plot the points O (0, 0), A (-4, 4), B (-3, 0) and C (0, -3)
(i) Reflect points A and B on the y-axis and name them A’ and B’ respectively. Write down their coordinates.
(ii) Name the figure OABCB’A’.
(iii) State the line of symmetry of this figure.
Solution:
1. A’ = (4, 4) AND B’ = (3, 0)
2. The figure is an arrow head.
3. The y-axis i.e. x = 0 is the line of symmetry of figure OABCB’A’.
Question 17.
(i) Plotting A(0, 4), B(2, 3), C(1, 1) and D(2, 0).
(ii) Reflected points B'(-2, 3), C'(-1, 1) and D'(-2, 0).
(iii) The figure is symmetrical about x = 0