Selina Concise Mathematics Class 9 ICSE Solutions Chapter 12 - Mid-point and Its Converse [ Including Intercept Theorem]

Selina Concise Mathematics Class 9 ICSE Solutions Mid-point and Its Converse [ Including Intercept Theorem]

Selina ICSE Solutions for Class 9 Maths Chapter 12 Mid-point and Its Converse [ Including Intercept Theorem]

Exercise 12(A)


1.In triangle ABC, M is mid-point of AB and a straight line through M and parallel to BC cuts AC in N. Find the lengths of AN and MN if Bc = 7 cm and Ac = 5 cm.

Solution 1:

2.Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.

Solution 2:

3.D, E and F are the mid-points of the sides AB, BC and CA of an isosceles ABC in which AB = BC. Prove that DEF is also isosceles.

Solution 3:

4.The following figure shows atrapezium ABCD in which AB // DC. P is the mid-point of AD and PR // AB. Prove that:

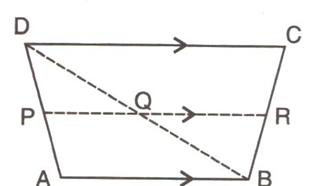
Solution 4:

5.The figure, given below, shows a trapezium ABCD. M and N are the mid-point of the non-parallel sides AD and BC respectively. Find:



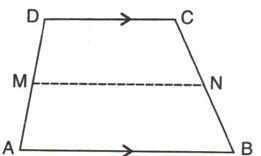
(i) MN, if AB = 11 cm and DC = 8 cm.

(ii) AB, if Dc = 20 cm and MN = 27 cm.

(iii) DC, if MN = 15 cm and AB = 23 cm.

Solution 5:

6.The diagonals of a quadrilateral intersect at right angles. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is rectangle.

Solution 6:

7.L and M are the mid-point of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.

Solution 7:

8.ABCD is a quadrilateral in which AD = BC. E, F, G and H are the mid-points of AB, BD, CD and Ac respectively. Prove that EFGH is a rhombus.



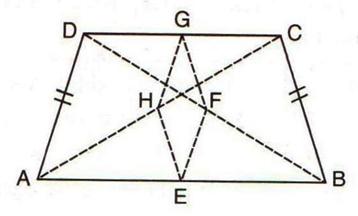
Solution 8:

9.A parallelogram ABCD has P the mid-point of Dc and Q a point of Ac such that CQ = AC. PQ produced meets BC at R.

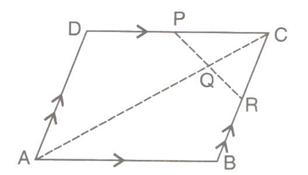
Prove that

(i)R is the midpoint of BC

(ii)

Solution 9:

10.D, E and F are the mid-points of the sides AB, BC and CA respectively of ABC. AE meets DF at O. P and Q are the mid-points of OB and OC respectively. Prove that DPQF is a parallelogram.

Solution 10:

11.In triangle ABC, P is the mid-point of side BC. A line through P and parallel to CA meets AB at point Q; and a line through Q and parallel to BC meets median AP at point R. Prove that

(i)AP=2AR

(ii)BC=4QR

Solution 11:

12.In trapezium ABCD, AB is parallel to DC; P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E. Prove that:

(i) Point P bisects BE,

(ii) PQ is parallel to AB.

Solution 12:

13.In a triangle ABC, AD is a median and E is mid-point of median AD. A line through B and E meets AC at point F.

Prove that: AC = 3AF

Solution 13:

14.D and F are mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.

(i) Prove that BDFE is parallelogram

(ii) Find AB, if EF = 4.8 cm.

Solution 14:

15.In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E. Show that BE is also a median.

Solution 15:

16.In ∆ABC, E is mid-point of the median AD and BE produced meets side AC at point Q. Show that BE : EQ = 3:1.

Solution 16:

17.In the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF. Show that: EF = AC.

 

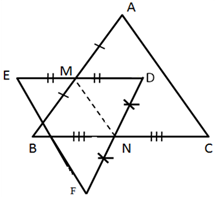
Solution 17:

Exercise 12(B)

1.Use the following figure to find:

(i) BC, if AB = 7.2 cm.

(ii) GE, if FE = 4 cm.

(iii) AE, if BD = 4.1 cm

(iv) DF, if CG = 11 cm.



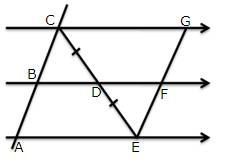
Solution 1:

2.In the figure, give below, 2AD = AB, P is mid-point of AB, Q is mid-point of DR and PR // BS. Prove that:

(i) AQ // BS

(ii) DS = 3 Rs.



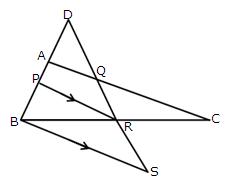
Solution 2:

3.The side AC of a triangle ABC is produced to point E so that CE = AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively. Prove that:

(i) 3DF = EF(ii) 4CR = AB.

Solution 3:

4.In triangle ABC, the medians BP and CQ are produced upto points M and N respectively such that BP = PM and CQ = QN. Prove that:

(i) M, A and N are collinear.

(ii) A is the mid-point of MN.

Solution 4:

5.In triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.

Solution 5:

6.In parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The line segments AF and BF meet the line segments ED and EC at points G and H respectively. Prove that:

(i) Triangles HEB and FHC are congruent;

(ii) GEHF is a parallelogram.

Solution 6:

7.In triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meet side BC at points M and N respectively. Prove that: BM = MN = NC.

Solution 7:

8.In triangle ABC; M is mid-point of AB, N is mid-point of AC and D is any point in base BC. Use intercept Theorem to show that MN bisects AD.

Solution 8:

9.If the quadrilateral formed by joining the mid-points of the adjacent sides of quadrilateral ABCD is a rectangle, show that the diagonals AC and BD intersect at right angle.

Solution 9:

10.In triangle ABC; D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm, find the perimeter of the parallelogram BDEF.

Solution 10:

11.In the given figure, AD and CE are medians and DF//CE. Prove that: 

 

Solution 11:

12.In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P.

 Prove that:

(i) BP = 2AD

 (ii) O is the mid-point of AP.




Solution 12:

Given ABCD is parallelogram, so AD = BC, AB = CD.
Consider triangle APB, given EC is parallel to AP and E is midpoint of side AB. So by midpoint theorem, C has to be the midpoint of BP.
So BP = 2BC, but BC = AD as ABCD is a parallelogram.
Hence BP = 2AD
Consider triangle APB, AB || OC as ABCD is a parallelogram. So by midpoint theorem, O has to be the midpoint of AP.
Hence Proved

13.In trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC. Prove that: AB + DC = 2EF.

Solution 13:

Consider trapezium ABCD.
Given E and F are midpoints on sides AD and BC, respectively.

Consider LHS,
AB + CD = AB + CJ + JI + ID = AB + 2HF + AB + 2EG
So AB + CD = 2(AB + HF + EG) = 2(EG + GH + HF) = 2EF
AB + CD = 2EF
Hence Proved

14.In Δ ABC, AD is the median and DE is parallel to BA, where E is a point in AC. Prove that BE is also a median.

Solution 14:

Given Δ ABC
AD is the median. So D is the midpoint of side BC.
Given DE || AB. By the midpoint theorem, E has to be midpoint of AC.
So line joining the vertex and midpoint of the opposite side is always known as median. So BE is also median of Δ ABC.

Selina Concise Mathematics Class 9 ICSE Solutions Chapter 12 - Mid-point and Its Converse [ Including Intercept Theorem]