Selina Concise Mathematics Class 9 ICSE Maths Solutions Chapter 23 - Trigonometrical Ratios of Standard Angles

Selina Concise Mathematics Class 9 ICSE Solutions Trigonometrical Ratios of Standard Angles

Selina ICSE Solutions for Class 9 Maths Chapter 23 Trigonometrical Ratios of Standard Angles [Including Evaluation of an Expression Involving Trigonometric Ratios]

Exercise 23(A)

1.find the value of:

(i) sin 30^o cos 30^o

(ii) tan 30^o tan 60^o

(iii) cos² 60^o + sin² 30^o

(iv) cosec² 60^o - tan² 30^o

(v) sin² 30^o + cos² 30^o + cot² 45^o

(vi) cos² 60^o + sec² 30^o + tan² 45^o.

Solution 1:

2.find the value of :

(i) tan² 30^o + tan² 45^o + tan² 60^o

(ii)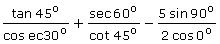 

(iii) 3 sin² 30^o + 2 tan² 60^o - 5 cos² 45^o.

Solution 2:

3.Prove that:

(i) sin 60^o cos 30^o + cos 60^o. sin 30^o = 1

(ii) cos 30^o. cos 60^o - sin 30^o. sin 60^o = 0

(iii) cosec² 45^o - cot² 45^o = 1

(iv) cos² 30^o - sin² 30^o = cos 60^o.

(v)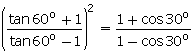 

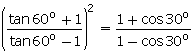
(vi) 3 cosec² 60^o - 2 cot² 30^o + sec² 45^o = 0.

Solution 3:

4.prove that:

(i) sin (2 30^o) = 

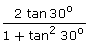
(ii) cos (2 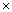30^o) =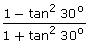 

(iii) tan (2 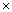30^o) =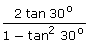 

Solution 4:

5.ABC is an isosceles right-angled triangle. Assuming of AB = BC = x, find the value of each of the following trigonometric ratios:

(i) sin 45^o

(ii) cos 45^o

(iii) tan 45^o

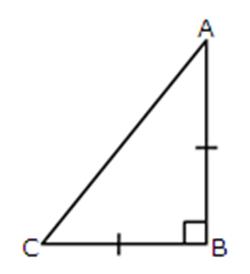
Solution 5:

6.Prove that:

(i) sin 60^o = 2 sin 30^o cos 30^o.

(ii) 4 (sin⁴ 30^o + cos⁴ 60^o)

-3 (cos² 45^o - sin² 90^o) = 2

Solution 6:

7.(i) If sin x = cos x and x is acute, state the value of x.

(ii) If sec A = cosec A and 0^o 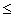A 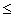90^o, state the value of A.

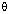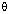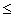
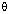
(iii) If tan = cot and 0^o 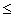90^o, state the value of.

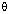(iv) If sin x = cos y; write the relation between x and y, if both the angles x and y are acute.

Solution 7:

8.(i) If sin x = cos y, then x + y = 45^o ; write true of false.

(ii) sec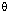. Cot 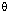= cosec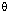; write true or false.

(iii) For any angle 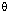, state the value of :

Sin² 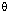+ cos².

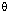Solution 8:

9.State for any acute angle 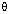 whether:

(i) sin 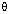 increases or decreases as  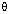increases:

(ii) cos 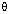 increases or decreases as  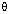increases.

(iii) tan 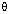 increases or decreases as  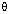decreases.

Solution 9:
(i) For acute angles, remember what sine means: opposite over hypotenuse. If we increase the angle, then the opposite side gets larger. That means “opposite/hypotenuse” gets larger or increases.
(ii) For acute angles, remember what cosine means: base over hypotenuse. If we increase the angle, then the hypotenuse side gets larger. That means “base/hypotenuse” gets smaller or decreases.
(iii) For acute angles, remember what tangent means: opposite over base. If we decrease the angle, then the opposite side gets smaller. That means “opposite /base” gets decreases.

10.If  = 1.732, find (correct to two decimal place) the value of each of the following:

(i) sin 60^o (ii)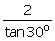 

Solution 10:

11.Evaluate:

(i) 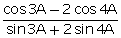, when A = 15^o.

(ii) 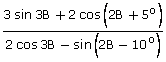 ; w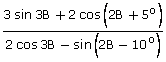hen B = 20^o.

Solution 11:

Exercise 23(B)

1.Given A = 60^o and B = 30^o, prove that:

(i) sin (A + B) = sin A cos B + cos A sin B

(ii) cos (A + B) = cos A cos B - sin A sin B

(iii) cos (A - B) = cos A cos B + sin A sin B

(iv) tan (A - B) =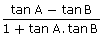 

Solution 1:

2.If A =30^o, then prove that:

(i) sin 2A = 2sin A cos A =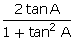 

(ii) cos 2A = cos²A - sin²A

= 

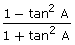
(iii) 2 cos² A - 1 = 1 - 2 sin²A

(iv) sin 3A = 3 sin A - 4 sin³A.

Solution 2:

3.If A = B = 45^o, show that:

(i) sin (A - B) = sin A cos B - cos A sin B

(ii) cos (A + B) = cos A cos B - sin A sin B

Solution 3:

4.If A = 30^o; show that:

(i) sin 3 A

= 4 sin A sin (60^o - A) sin (60^o + A)

(ii) (sin A - cos A)² = 1 - sin 2A

(iii) cos 2A = cos⁴ A - sin⁴ A

(iv)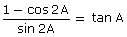 

(v) 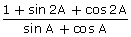= 2 cos A.

(vi) 4 cos A cos (60^o - A). cos (60^o + A)

= cos 3A

(vii)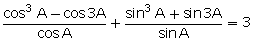 

Solution 4:

Exercise 23(C)

1.Solve the following equations for A, if :

(i) 2 sin A = 1 (ii) 2 cos 2 A = 1

(iii) sin 3 A = 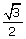 (iv) sec 2 A = 2

(v) 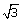 tan A = 1 (vi) tan 3 A = 1

(vii) 2 sin 3 A = 1 (viii) 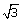 cot 2 A = 1

Solution 1:

2.Calculate the value of A, if :

(i) (sin A - 1) (2 cos A - 1) = 0

(ii) (tan A - 1) (cosec 3A - 1) = 0

(iii) (sec 2A - 1) (cosec 3A - 1) = 0

(iv) cos 3A. (2 sin 2A - 1) = 0

(v) (cosec 2A - 2) (cot 3A - 1) = 0

Solution 2:

3.If 2 sin x^o - 1 = 0 and x^o is an acute angle; find :

(i) sin x^o (ii) x^o (iii) cos x^o and tan x^o.

Solution 3:

4.If 4 cos² x^o - 1 = 0 and 0 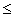 x^o 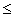 90^o, find:

(i) x^o (ii) sin² x^o + cos² x^o

(iii)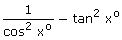 

Solution 4:

5.If 4 sin² 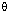 - 1= 0 and angle  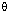is less than 90^o, find the value of  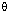and hence the value of cos²  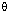+ tan².

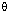Solution 5:

6.If sin 3A = 1 and 0 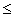 A 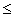 90^o, find:

(i) sin A (ii) cos 2A

(iii) tan²A -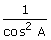 

Solution 6:

7.If 2 cos 2A = 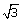 and A is acute, find:

(i) A (ii) sin 3A

(iii) sin² (75^o - A) + cos² (45^o +A)

Solution 7:

8.(i) If sin x + cos y = 1 and x = 30^o, find the value of y.

(ii) If 3 tan A - 5 cos B= 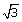 and B = 90^o, find the value of A.

Solution 8:

9.From the given figure, find:

(i) cos x^o(ii) x^o

(iii)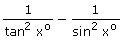 

(iv) Use tan x^o, to find the value of y.

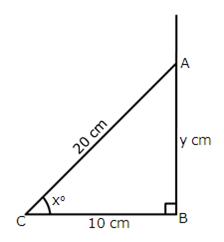
Solution 9:

10.Use the given figure to find:

(i) tan 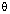^o (ii) 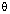^o (iii) sin^2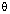o - cos^2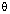o

(iv) Use sin 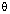^o to find the value of x.

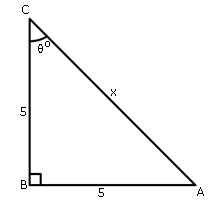
Solution 10:

11.Find the magnitude of angle A, if:

(i) 2 sin A cos A - cos A - 2 sin A + 1 = 0

(ii) tan A - 2 cos A tan A + 2 cos A - 1 = 0

(iii) 2 cos² A - 3 cos A + 1 = 0

(iv) 2 tan 3A cos 3A - tan 3A + 1 = 2 cos 3A

Solution 11:

12.Solve for x:

(i) 2 cos 3x - 1 = 0 (ii) cos 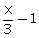 = 0

(iii) sin (x + 10^o) = 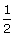 (iv) cos (2x - 30^o) = 0

(v) 2 cos (3x - 15^o) = 1 (vi) tan² (x - 5^o) = 3

(vii) 3 tan² (2x - 20^o) = 1

(viii) cos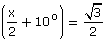 

(ix) sin² x + sin² 30^o = 1

(x) cos² 30^o + cos² x = 1

(xi) cos² 30^o + sin² 2x = 1

(xii) sin² 60^o + cos² (3x- 9^o) = 1

Solution 12:

13.If 4 cos² x = 3 and x is an acute angle; find the value of :

(i) x (ii) cos² x + cot² x

(iii) cos 3x (iv) sin 2x

Solution 13:

14.In ABC, 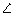B = 90^o, AB = y units, BC =  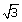units, AC = 2 units and angle A = x^o, find:

(i) sin x^o (ii) x^o (iii) tan x^o

(iv) use cos x^o to find the value of y.

Solution 14:

15.If 2 cos (A + B) = 2 sin (A - B) = 1; find the values of A and B.

Solution 15:

Selina Concise Mathematics Class 9 ICSE Maths Solutions Chapter 23 - Trigonometrical Ratios of Standard Angles