Selina Concise Physics Class 10 ICSE Solutions Machines
Selina ICSE Solutions for Class 10 Physics Chapter 3 Machines
Exercise 3(A)
1.(a) What do you understand by a simple machine?
(b) State the principle of an ideal machine.
Solution 1.
(a) A machine is a device by which we can either overcome a large resistive force at some point by applying a small force at a convenient point and in a desired direction or by which we can obtain a gain in the speed.
(b) An ideal machine is a machine whose parts are weightless and frictionless so that which there is no dissipation of energy in any manner. Its efficiency is 100%, i.e. the work output is equal to work input.
2.State four ways in which machines are useful to us?
Solution 2.
Machines are useful to us in the following ways:
- In lifting a heavy load by applying a less effort.
- In changing the point of application of effort to a convenient point.
- In changing the direction of effort to a convenient direction.
- For obtaining a gain in speed.
3.Name the machine for each of the following use:
(a) to multiply the force,
(b) to change the point of application of force,
(c) to change the direction of force,
(d) to obtain the gain in speed.
(a) to multiply the force,
(b) to change the point of application of force,
(c) to change the direction of force,
(d) to obtain the gain in speed.
Solution 3.
(a) To multiply force: a jack is used to lift a car.
(b) To change the point of application of force: the wheel of a cycle is rotated with the help of a chain by applying the force on the pedal.
(c) To change the direction of force: a single fixed pulley is used to lift a bucket full of water from the well by applying the effort in the downward direction instead of applying it upwards when the bucket is lifted up without the use of pulley.
(d) To obtain gain in speed: when a pair of scissors is used to cut the cloth, its blades move longer on cloth while its handles move a little.
4.What is the purpose of a jack in lifting a car by it?
4.What is the purpose of a jack in lifting a car by it?
Solution 4.
The purpose of jack is to make the effort less than the load so that it works as a force multiplier.
5.Explain the term mechanical advantage. State its unit.
5.Explain the term mechanical advantage. State its unit.
Solution 5.
The ratio of the load to the effort is called mechanical advantage of the machine. It has no unit.
6.Define the term velocity ratio. State its unit.
Solution 6.
The ratio of the velocity of effort to the velocity of the load is called the velocity ratio of machine. It has no unit.
7.How is mechanical advantage related to the velocity ratio for (i) an ideal machine, (ii) a practical machine?
7.How is mechanical advantage related to the velocity ratio for (i) an ideal machine, (ii) a practical machine?
Solution 7.
For an ideal machine mechanical advantage is numerically equal to the velocity ratio.
8.Define the term efficiency of a machine. Give two reasons for a machine not to be 100% efficient?
Solution 8.
It is the ratio of the useful work done by the machine to the work put into the machine by the effort.
In actual machine there is always some loss of energy due to friction and weight of moving parts, thus the output energy is always less than the input energy.
9.When does a machine act as (a) a force multiplier and (b) a speed multiplier? Can a machine act as a force multiplier and speed multiplier simultaneously?
9.When does a machine act as (a) a force multiplier and (b) a speed multiplier? Can a machine act as a force multiplier and speed multiplier simultaneously?
Solution 9.
(a) A machine acts as a force multiplier when the effort arm is longer than the load arm. The mechanical advantage of such machines is greater than 1.
(b) A machine acts a speed multiplier when the effort arm is shorter than the load arm. The mechanical advantage of such machines is less than 1.
It is not possible for a machine to act as a force multiplier and speed multiplier simultaneously. This is because machines which are force multipliers cannot gain in speed and vice-versa.
10.(a) State the relationship between mechanical advantage, velocity ratio and efficiency.
(b) Name the term that will not change for a machine of a given design.
10.(a) State the relationship between mechanical advantage, velocity ratio and efficiency.
(b) Name the term that will not change for a machine of a given design.
Solution 10.
11.Derive the relationship between mechanical advantage, velocity ratio and efficiency of a machine.
Solution 11.
Let a machine overcome a load L by the application of an effort E. In time t, let the displacement of effort be dE and the displacement of load be dL.
Work input = Effort X displacement of effort = E X dE
Work output = Load X displacement of load = L X dL
12.How is the mechanical advantage related with the velocity ratio for an actual machine? State whether the efficiency of such a machine is equal to 1, less than 1 or more than 1.
Solution 12.
13.State one reason why is mechanical advantage less than the velocity ratio for an actual machine.
Solution 13
This is because the output work is always less than the input work, so the efficiency is always less than 1 because of energy loss due to friction.
14.What is a lever? State its principle.
Solution 14.
A lever is a rigid, straight or bent bar which is capable of turning about a fixed axis.
Principle: A lever works on the principle of moments. For an ideal lever, it is assumed that the lever is weightless and frictionless. In the equilibrium position of the lever, by the principle of moments,
Moment of load about the fulcrum = Moment of the effort about the fulcrum.
15.Write down a relation expressing the mechanical advantage of a lever.
15.Write down a relation expressing the mechanical advantage of a lever.
Solution 15.
16.Name the three classes of levers and state how are they distinguished. Give two examples of each class.
Solution 16.
The three classes of levers are:
- Class I levers: In these types of levers, the fulcrum F is in between the effort E and the load L. Example: a seesaw, a pair of scissors, crowbar.
- Class II levers: In these types of levers, the load L is in between the effort E and the fulcrum F. The effort arm is thus always longer than the load arm. Example: a nut cracker, a bottle opener.
- Class III levers: In these types of levers, the effort E is in between the fulcrum F and the load L and the effort arm is always smaller than the load arm. Example: sugar tongs, forearm used for lifting a load.
17.Give one example each of a class I lever where mechanical advantage is (a) more than 1, and (b) less than 1.
Solution 17.
(a) More than one: shears used for cutting the thin metal sheets.
(b) Less than one: a pair of scissors whose blades are longer than its handles.
18.What is the use of lever if its mechanical advantage is (a) more than 1, (b) equal to 1, and (c) less than 1?
18.What is the use of lever if its mechanical advantage is (a) more than 1, (b) equal to 1, and (c) less than 1?
Solution 18.
When the mechanical advantage is less than 1, the levers are used to obtain gain in speed. This implies that the displacement of load is more as compared to the displacement of effort.
19.Both a pair of scissors and a pair of pliers belong to the same class of levers. Name the class of lever. Which one has the mechanical advantage less than 1?
19.Both a pair of scissors and a pair of pliers belong to the same class of levers. Name the class of lever. Which one has the mechanical advantage less than 1?
Solution 19.
A pair of scissors and a pair of pliers both belong to class I lever.
A pair of scissors has mechanical advantage less than 1.
20.Explain why scissors for cutting cloth may have blades longer than the handles, but shears for cutting metals have short blades and long handles.
20.Explain why scissors for cutting cloth may have blades longer than the handles, but shears for cutting metals have short blades and long handles.
Solution 20.
A pair of scissors used to cut a piece of cloth has blades longer than the handles so that the blades move longer on the cloth than the movement at the handles.
While shears used for cutting metals have short blades and long handles because as it enables us to overcome large resistive force by a small effort.
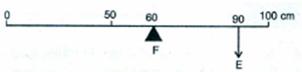
21.Figure shows a uniform metre scale of weight W supported on a fulcrum at the 60 cm mark by applying the effort E at the 90 cm mark.
(a) State with reasons whether the weight W of the rule is greater than, less than or equal to the effort E.
(b) Find the mechanical advantage in an ideal case.
21.Figure shows a uniform metre scale of weight W supported on a fulcrum at the 60 cm mark by applying the effort E at the 90 cm mark.
(a) State with reasons whether the weight W of the rule is greater than, less than or equal to the effort E.
(b) Find the mechanical advantage in an ideal case.
Solution 21.
(a) The weight W of the scale is greater than E.
It is because arm on the side of effort E is 30 cm and on the side of weight of scale is 10 cm. So, to balance the scale, weight W of scale should be more than effort E.
22.Which type of lever has a mechanical advantage always more than 1? Give reason with one example. What change can be made in this lever to increase its mechanical advantage?
Solution 22.
Class II lever always have a mechanical advantage more than one.
Example: a nut cracker.
To increase its mechanical advantage we can increase the length of effort arm.
23.Draw a diagram of a lever which is always used as a force multiplier. How is the effort arm related to the load arm in such a lever?
23.Draw a diagram of a lever which is always used as a force multiplier. How is the effort arm related to the load arm in such a lever?
Solution 23.
24.Explain why the mechanical advantage of a class II type of lever is always more than 1.
Solution 24.
In these types of levers, the load L is in between the effort E and the fulcrum F. So, the effort arm is thus always longer than the load arm. Therefore M.A > 1.
25.Draw a labelled diagram of a Class II lever. Give one example of such a lever.
25.Draw a labelled diagram of a Class II lever. Give one example of such a lever.
Solution 25.
26.
Solution 26.
27.State the kind of lever which always has the mechanical advantage less than 1. Draw a labelled diagram of such lever.
Solution 27.
28.Explain why the mechanical advantage of the class III type of lever is always less than 1.
Solution 28..
In these types of levers, the effort is in between the fulcrum F and the load L and so the effort arm is always smaller than the load arm. Therefore M.A. < 1.
29.Classes III levers have mechanical advantage less than 1. Why are they then used?
29.Classes III levers have mechanical advantage less than 1. Why are they then used?
Solution 29.
With levers of class III, we do not get gain in force, but we get gain in speed, that is a longer displacement of load is obtained by a smaller displacement of effort.
30.Draw a labelled sketch of a class III lever. Give one example of this kind of lever.
30.Draw a labelled sketch of a class III lever. Give one example of this kind of lever.
Solution 30.
31.State the class of levers and the relative positions of load (L), effort (E) and fulcrum (F) in (a) a bottle opener, and (b) sugar tongs.
Solution 31.
(a) A bottle opener is a lever of the second order, as the load is in the middle, fulcrum at one end and effort at the other.
(b) Sugar tongs is a lever of the third order as the effort is in the middle, load at one end and fulcrum at the other end.
32.Draw diagrams to illustrate the position of fulcrum, load and effort, in each of the following:
(a)A seesaw
(b)A common balance
(c)A nut cracker
(d)Forceps.
Solution 32.
33.Classify the following into levers as class I, class II or class III:
(a) A door (b) a catapult (c) a wheel barrow (d) a fishing rod.
Solution 33.
a. Class II
b. Class I
c. Class II
d. Class III
34.What type of lever is formed by the human body while (a) raising a load on the palm, and (b) raising the weight of body on toes?
34.What type of lever is formed by the human body while (a) raising a load on the palm, and (b) raising the weight of body on toes?
Solution 34.
(a) Class III.
Here, the fulcrum is the elbow of the human arm. Biceps exert the effort in the middle and load on the palm is at the other end.
(b) Class II.
Here, the fulcrum is at toes at one end, the load (i.e. weight of the body) is in the middle and effort by muscles is at the other end.
35.Indicate the positions of load L, effort E and fulcrum F in the forearm shown below. Name the class of lever.
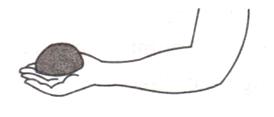
Solution 35.
36.Give example of each class of lever in a human body.
Solution 36.
Class I lever in the action of nodding of the head: In this action, the spine acts as the fulcrum, load is at its front part, while effort is at its rear part.
Class II lever in raising the weight of the body on toes: The fulcrum is at toes at one end, the load is in the middle and effort by muscles is at the other end.
Class III lever in raising a load by forearm: The elbow joint acts as fulcrum at one end, biceps exerts the effort in the middle and a load on the palm is at the other end.
1(MCQ).Mechanical advantage (M.A.), load (L) and effort (E) are related as:
1(MCQ).Mechanical advantage (M.A.), load (L) and effort (E) are related as:
a. M.A. = L x E
b. M.A. x E = L
c. E = M.A. x L
d. None of these
Solution 1 (MCQ).
M.A. x E = L
2(MCQ).The correct relationship between the mechanical advantage (M.A.), velocity ratio (V.R.) and efficiency (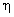
) is:
2(MCQ).The correct relationship between the mechanical advantage (M.A.), velocity ratio (V.R.) and efficiency (
) is:
a. M.A. = x V.R.
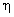x V.R.
b. V.R. = 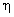x M.A.
x M.A.
c. 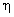=M.A. x V.R.
=M.A. x V.R.
d. None of these
Solution 2 (MCQ).
3(MCQ).State the incorrect statement:
A machine always has the efficiency less than 100%.
The mechanical advantage of a machine can be less than 1.
A machine can be used as speed multiplier.
A machine can have the mechanical advantage greater than the velocity ratio.
Solution 3 (MCQ).
It can have a mechanical advantage greater than the velocity ratio.
Reason: If the mechanical advantage of a machine is greater than its velocity ratio, then it would mean that the efficiency of a machine is more than 100%, which is practically not possible.
4(MCQ).The lever for which the mechanical advantage is less than 1 has the :
Fulcrum at mid-point between load and effort.
Load between effort and fulcrum.
Effort between fulcrum and load.
Load and effort acting at the same point.
4(MCQ).The lever for which the mechanical advantage is less than 1 has the :
Fulcrum at mid-point between load and effort.
Load between effort and fulcrum.
Effort between fulcrum and load.
Load and effort acting at the same point.
Solution 4 (MCQ).
Effort is between fulcrum and load
Hint: Levers, for which the mechanical advantage is less than 1, always have the effort arm shorter than the load arm.
5(MCQ).Class II levers are designed to have:
5(MCQ).Class II levers are designed to have:
a. M.A. = V.R.
b. M.A. > V.R.
c. M.A. > 1
d. M.A. < 1
Solution 5 (MCQ).
M.A > 1
Hint: In class II levers, the load is in between the effort and fulcrum. Thus, the effort arm is always longer than the load arm and less effort is needed to overcome a large load. Hence, M.A > 1.
Numericals
1.A crowbar of length 120 cm has its fulcrum situated at a distance of 20 cm from the load. Calculate the mechanical advantage of the crowbar.
Solution 1.
2.A pair of scissors has its blades 15 cm long, while its handles are 7.5 cm long. What is its mechanical advantage?
Solution 2.
3.A force of 5kgf is required to cut a metal sheet. A shears used for cutting the metal sheet has its blades 5 cm long, while its handle is 10 cm long. What effort is needed to cut the sheet?
Solution 3.
4.The diagram below shows a lever in use.
To which class of lever does it belong?
If AB =1 m, AF= 0.4 m, find its mechanical advantage.
Calculate the value of E.
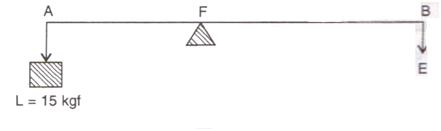
Solution 4.
5.A man uses a crowbar of length 1.5 m to raise a load of 75kgf by putting a sharp edge below the bar at a distance 1 m from his hand. (a) Draw a diagram of the arrangement showing the fulcrum (F), load (L) and effort (E) with their directions. (b) State the kind of lever. (c) Calculate: (i) load arm, (ii) effort arm, (iii) mechanical advantage, and (iv) the effort needed.
Solution 5.
6.A pair of scissors is used to cut a piece of a cloth by keeping it at a distance 8.0 cm from its rivet and applying an effort of 10 kgf by fingers at a distance 2.0 cm from the rivet.
(a) Find: (i) the mechanical advantage of scissors and (ii) the load offered by the cloth.
(b) How does the pair of scissors act: as a force multiplier or as a speed multiplier?
Solution 6.
7.A 4 m long rod of negligible weight is to be balanced about a point 125 cm from one end and A load of 18 kgf is suspended at a point 60 cm from the support on the shorter arm.
(a) If a weight W is placed at a distance of 250 cm from the support on the longer arm, Find W.
(b) If a weight 5 kgf is kept to balance the rod, find its position.
(c) To which class of lever does it belong?
Solution 7.
Total length of rod=4 m = 400 cm
(a) 18kgf load is placed at 60 cm from the support.
W kgf weight is placed at 250 cm from the support.
By the principle of moments
18 x 60 = W x 250
W = 4.32 kgf
(b) Given W=5 kgf
18kgf load is placed at 60 cm from the support.
Let 5 kgf of weight is placed at d cm from the support.
By the principle of moments
18 x 60 = 5 x d
d = 216 cm from the support on the longer arm
(c) It belongs to class I lever.
8.The diagram below shows a lever in use.
(a) To which class of lever does it belong?
(b) If FA = 80 cm, AB = 20 cm, find its mechanical advantage.
(c) Calculate the value of E.
8.The diagram below shows a lever in use.
(a) To which class of lever does it belong?
(b) If FA = 80 cm, AB = 20 cm, find its mechanical advantage.
(c) Calculate the value of E.
Solution 8.
9.The figure shows a wheel barrow of mass 15 kg carrying a load of 30 kgf with its center of gravity at A. The points B and C are the centre of wheel and tip of the handle such that the horizontal distance AB = 20 cm and AC = 40 cm.
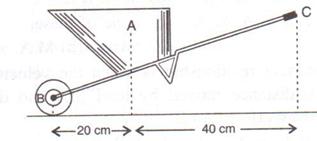
Find: (a) the load arm, (b) the effort arm, (c) the mechanical advantage, and (d) the
minimum effort required to keep the leg just off the ground.
Solution 9.
10.The diagram below shows the use of a lever.
(a) State the principle of moments as applied to the above lever.
(b) To which class of lever does it belong? Give an example of this class of lever.
(c) If FA = 10cm, AB = 490cm, calculate: (i) the mechanical advantage, and (ii) the minimum effort required to lift the load (= 50N).
Solution 10.
(a) The principle of moments: Moment of the load about the fulcrum=moment of the effort about the fulcrum
FB x Load = FA x Effort
(b) Sugar tongs the example of this class of lever.
(c) Given: FA=10 cm, AB = 500 cm, BF =500+10=510 cm.
The mechanical advantage
11.A fire tongs has its arms 20 cm long. It is used to lift a coal of weight 1.5kgf by applying an effort at a distance 15 cm from the fulcrum. Find: (i) the mechanical advantage of fire tongs and (ii) the effort needed.
Solution 11.
Exercise 3(B)
1.What is a fixed pulley? State its one use.
Solution 1.
Fixed pulley: A pulley which has its axis of rotation fixed in position, is called a fixed pulley.
Single fixed pulley is used in lifting a small load like water bucket from the well.
2.What is the ideal mechanical advantage of a single fixed pulley? Can it be used as a force multiplier?
2.What is the ideal mechanical advantage of a single fixed pulley? Can it be used as a force multiplier?
Solution 2.
The ideal mechanical advantage of a single fixed pulley is 1.
It cannot be used as force multiplier.
3.Name the pulley which has no gain in mechanical advantage. Explain, why is such a pulley is then used?
3.Name the pulley which has no gain in mechanical advantage. Explain, why is such a pulley is then used?
Solution 3.
There is no gain in mechanical advantage in the case of a single fixed pulley. A single fixed pulley is used only to change the direction of the force applied that is with its use, the effort can be applied in a more convenient direction. To raise a load directly upwards is difficult.
4.What is the velocity ratio of a single fixed pulley?
4.What is the velocity ratio of a single fixed pulley?
Solution 4.
The velocity ratio of a single fixed pulley is 1.
5.In a single fixed pulley, if the effort moves by a distance x downwards, by what height is the load raised upwards?
5.In a single fixed pulley, if the effort moves by a distance x downwards, by what height is the load raised upwards?
Solution 5.
The load rises upwards with the same distance x.
6.What is a single movable pulley? What is its mechanical advantage in the ideal case?
6.What is a single movable pulley? What is its mechanical advantage in the ideal case?
Solution 6.
Single movable pulley: A pulley, whose axis of rotation is not fixed in position, is called a single movable pulley.
Mechanical advantage in the ideal case is 2.
7.Give two reasons why the efficiency of a single movable pulley system is not 100%.
7.Give two reasons why the efficiency of a single movable pulley system is not 100%.
Solution 7.
The efficiency of a single movable pulley system is not 100% this is because
- The friction of the pulley bearing is not zero ,
- The weight of the pulley and string is not zero.
8.In which direction the force need be applied, when a single pulley is used with a mechanical advantage greater than 1? How can you change the direction of force applied without altering its mechanical advantage? Draw a labelled diagram of the system.
Solution 8.
The force should be in upward direction.
The direction of force applied can be changed without altering its mechanical advantage by using a single movable pulley along with a single fixed pulley to change the direction of applied force.
Diagram:
9.What is the velocity ratio of a single movable pulley? How does the friction in the pulley bearing affect it?
Solution 9.
The velocity ratio of a single movable pulley is always 2.
10.In a single movable pulley, if the effort moves by a distance x upwards, by what height is the load raised?
10.In a single movable pulley, if the effort moves by a distance x upwards, by what height is the load raised?
Solution 10.
The load is raised to a height of x/2.
11.Draw a labelled diagram of an arrangement of two pulleys, one fixed and other moveable. In the diagram, mark the directions of all forces acting on it. What is the ideal mechanical advantage of the system? How can it be achieved?
11.Draw a labelled diagram of an arrangement of two pulleys, one fixed and other moveable. In the diagram, mark the directions of all forces acting on it. What is the ideal mechanical advantage of the system? How can it be achieved?
Solution 11.
Ideal mechanical advantage of this system is 2. This can be achieved by assuming that string and the pulley are massless and there is no friction in the pulley bearings or at the axle or between the string and surface of the rim of the pulley.
12.The diagram alongside shows a pulley arrangement.
(a) Name the pulleys A and B.
(b) In the diagram, mark the direction of tension on each strand of string.
(c) What is the purpose of the pulley B?
(d) If the tension is T, deduce the relation between (i) T and E, and (ii) E and L.
(e) What is the velocity ratio of the arrangement?
(f) Assuming that the efficiency of the system is 100%, what is the mechanical advantage?
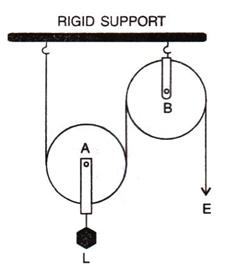
12.The diagram alongside shows a pulley arrangement.
(a) Name the pulleys A and B.
(b) In the diagram, mark the direction of tension on each strand of string.
(c) What is the purpose of the pulley B?
(d) If the tension is T, deduce the relation between (i) T and E, and (ii) E and L.
(e) What is the velocity ratio of the arrangement?
(f) Assuming that the efficiency of the system is 100%, what is the mechanical advantage?
Solution 12.
(b) The fixed pulley B is used to change the direction of effort to be applied from upward to downward.
(c) The effort E balances the tension T at the free end, so E=T
(d) The velocity ratio of this arrangement is 2.
(e) The mechanical advantage is 2 for this system (if efficiency is 100%).
13.State four differences between a single fixed pulley and a single movable pulley.
13.State four differences between a single fixed pulley and a single movable pulley.
Solution 13.
14.The diagram alongside shows and arrangement of three pulleys A, B and C. The load is marked as L and the effort as E.
(a) Name the pulleys A, B and C.
(b) Mark in the diagram the direction of load (L), effort (E) and tension T1 and T2 in the two strings.
(c) How are the magnitudes of L and E related to the tension T1?
(d) Calculate the mechanical advantage and velocity ratio of the arrangement.
(e) What assumptions have you made in parts (c) and (d)?
Solution 14.
15.Draw a diagram of combination of three movable pulleys and one fixed pulley to lift up a load. in the diagram, show the directions of load, effort and tension in each strand. Find: (i) the mechanical advantage, (ii) velocity ratio and (iii) the efficiency of the combination in ideal situation.
Solution 15.
As one end of each string passing over a movable pulley is fixed, so the free end of string moves twice the distance moved by the movable pulley.
If load L moves up by a distance x, dL = x, effort moves by a distance 23x, dE = 23x
Solution 16.
16.Draw a diagram of a block and tackle system of pulleys having a velocity ratio of 5. In your diagram indicate clearly the points of application and the directions of the load L and effort E. Also mark the tension T in each strand.
Solution 16.
17.Give reasons for the following :
(a) In a single fixed pulley, the velocity ratio is always more than the mechanical advantage.
(b) The efficiency of a movable pulley is always less than 100%.
(c) In case of block and tackle system, the mechanical advantage increases with the increase in the number of pulleys.
(d) The lower block of a block and tackle pulley system must be of negligible weight.
Solution 17.
- In a single fixed pulley, some effort is wasted in overcoming friction between the strings and the grooves of the pulley; so the effort needed is greater than the load and hence the mechanical advantage is less than the velocity ratio.
- This is because of some effort is wasted in overcoming the friction between the strings and the grooves of the pulley.
- This is because mechanical advantage is equal to the total number of pulleys in both the blocks.
- The efficiency depends upon the mass of lower block; therefore efficiency is reduced due to the weight of the lower block of pulleys.
18.Name the machine which is used to:
(a)Multiply force
(b)Multiplied speed, and
(c)Change the direction of force applied.
(a)Multiply force
(b)Multiplied speed, and
(c)Change the direction of force applied.
Solution 18.
(a) Multiply force: a movable pulley.
(b) Multiply speed: gear system or class III lever.
(c) Change the direction of force applied: single fixed pulley.
19.State whether the following statements are true or false.
The velocity ratio of a single fixed pulley is always more than 1.
The velocity ratio of a single movable pulley is always 2.
The velocity ratio of a combination of n movable pulleys with a fixed pulley is always 2n.
The velocity ratio of a block and tackle system is always equal to the number of strands of the tackle supporting the load.
Solution 19.
- The velocity ratio of a single fixed pulley is always more than 1.(false)
- The velocity ratio of a single movable pulley is always 2.(true)
- The velocity ratio of a combination of n movable pulleys with a fixed pulley is always 2n.(true)
- The velocity ratio of a block and tackle system is always equal to the number of strands of the tackle supporting the load. (true)
1(MCQ).A single fixed pulley is used because it:
(a) Has a mechanical advantage greater than 1
(b) Has a velocity ratio less than 1
(c) Gives 100% efficiency
(d) Helps to apply the effort in a convenient direction.
(a) Has a mechanical advantage greater than 1
(b) Has a velocity ratio less than 1
(c) Gives 100% efficiency
(d) Helps to apply the effort in a convenient direction.
Solution 1 (MCQ).
It helps in applying effort in a convenient direction.
Explanation: A single fixed pulley though does not reduce the effort but helps in changing the direction of effort applied. As it is far easier to apply effort in downward direction, the single fixed pulley is widely used.
2(MCQ).The mechanical advantage of an ideal single movable pulley is:
(a) 1
(b) 2
(3) less than 2
(4) less than 1.
2(MCQ).The mechanical advantage of an ideal single movable pulley is:
(a) 1
(b) 2
(3) less than 2
(4) less than 1.
Solution 2 (MCQ).
The mechanical advantage of an ideal single movable pulley is 2.
Derivation: Consider the diagram given below:
Here the load L is balance by the tension in two segments of the string and the effort E balances the tension T at the free end, so
L = T + T = 2T and E = T
Assumption: Weight of the pulley is negligible.
We know that,
3(MCQ).A movable pulley is used as :
(a) a force multiplier
(b) a speed multiplier
(c) a device to change the direction of effort
(d) an energy multiplier
Solution 3 (MCQ).
Force multiplier
Explanation: The mechanical advantage of movable pulley is greater than 1. Thus, using a single movable pulley, the load can be lifted by applying an effort equal to half the load (in ideal situation), i.e. the single movable pulley acts as a force multiplier.
Numericals
1.A woman draws water from a well using a fixed pulley. The mass of bucket and water together is 6 kg. The force applied by the women is 70 N. calculate the mechanical advantage. (Take g = 10 m s-2).
Solution 1.
2.
Solution 2.
3.In a block and tackle system consisting of 3 pulleys, a load of 75 kgf is raised with an effort of 25 kgf. Find: (i) the mechanical advantage, (ii) the velocity ratio, and (iii) the efficiency.
Solution 3.
4.A block and tackle system has 5 pulleys. If an effort of 1000 N is needed in the downward direction to raise a load of 4500 N, calculate:
(a)The mechanical advantage,
(b)The velocity ratio and,
(c)The efficiency of the system.
Solution 4.
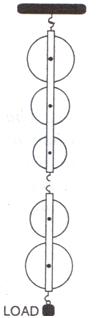
5.In figure draw a tackle to lift the load by applying the force in the download direction.
(a) Mark in the diagram the direction of load L and effort E.
(b) If the load is raised by 1 m, through what distance will the effort move?
(c) State how many strands of tackle are supporting the load.
(d) What is the mechanical advantage of the system?
Solution 5.
6.
Solution 6.
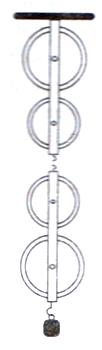
7. Figure shows a system of four pulleys. The upper two pulleys are fixed and the lower two are movable.
(a) Draw a string around the pulleys. Also show the point of application and direction in which the effort E is applied.
(b) What is the velocity ratio of the system?
(c) How are load and effort of the pulley system related?
(d) What assumption do you make in arriving at your answer in part (c)?
Solution 7.
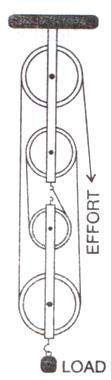
8.Figure shows a block and tackle system of pulleys used to lift a load.
(a) How many strands of tackle are supporting the load?
(b) Draw arrows to represent tension T in each strand.
(c) What is the mechanical advantage of the system?
(d) When load is pulled up by a distance 1 m, how far does the effort end move?
(e) How much effort is needed to lift a load of 100 N?
Solution 8.
9.
Solution 9.
10. You are given four pulleys and three strings. Draw a neat and labelled diagram to use them so as to obtain a maximum mechanical advantage equal to 8. In your diagram mark the directions of load L, effort E and tension in each strand.
What assumptions have you made to obtain the required mechanical advantage?
[Hint: Three movable pulleys with one fixed pulley]
Solution 10.
