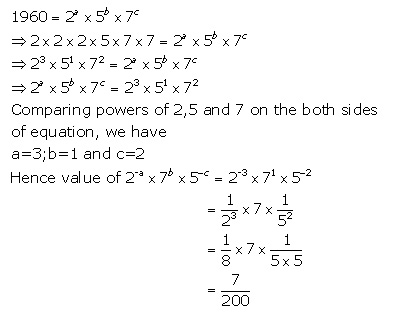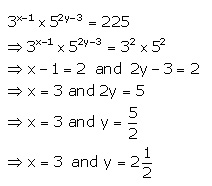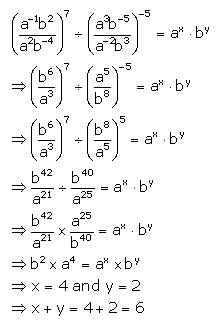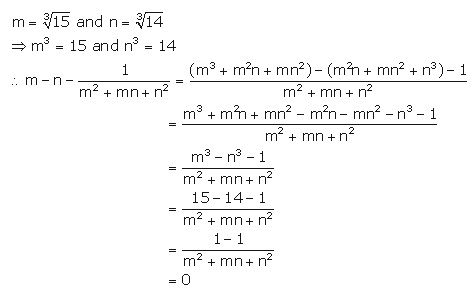Selina Concise Mathematics Class 9 ICSE Solutions Chapter 7- Indices (Exponents)

Selina Concise Mathematics Class 9 ICSE Solutions Indices (Exponents)

Selina ICSE Solutions for Class 9 Maths Chapter 7 Indices (Exponents)

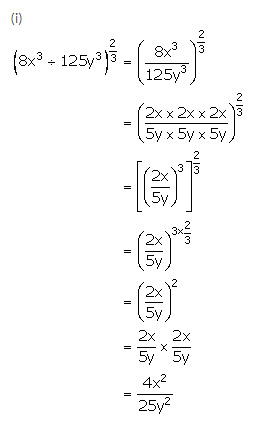
Exercise 7(A)

1.Evaluate:

(i)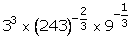 

(ii)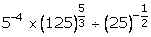 

(iii)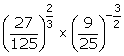 

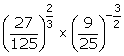
(iv)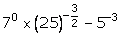 

(v)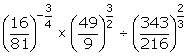 

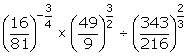
Solution 1:

2.Simplify:

(i)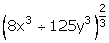 

(ii) 

(iii) 

(iv) 

Solution 2:

3.Evaluate:

(i)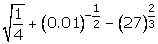 

(ii)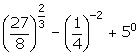 

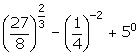
Solution 3:

4.Simplify each of the following and express with positive index:

(i)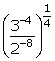 

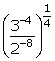
(ii)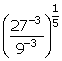 

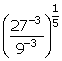
(iii)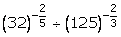 

(iv)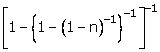 

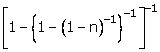
Solution 4:

5.If 2160 = 2^a. 3^b. 5^c, find a, b and c. Hence calculate the value of 3^a 2^-b 5^-c.

Solution 5:

6.If 1960 = 2^a. 5^b. 7^c, calculate the value of 2^-a. 7^b. 5^-c.

Solution 6:

7.Simplify:

(i)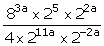 

(ii)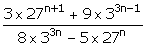 

Solution 7:

8.Show that:


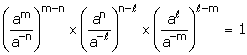
Solution 8:

9.If a = x^{m + n}. y^l; b = x^n + l. l ^. y^m and c = x^{l + m}. yⁿ,

Prove that: a^{m - n}. b^n - l. c^{l - m} = 1

Solution 9:

10.Simplify:

(i) 

(ii)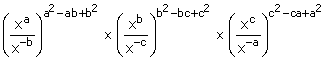 

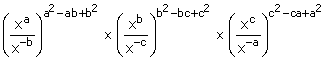
Solution 10:

Exercise 7(B)

1.Solve for x:

(i) 2^2x+1 = 8

(ii) 2^5x-1 = 4 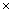2^{3x + 1}

(iii) 3^{4x + 1} = (27)^{x + 1}

(iv) (49)^{x + 4} = 7²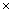 (343)^{x + 1}

Solution 1:

2.Find x, if:

(i) 

(ii)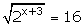 

(iii)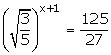 

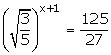
(iv)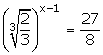 

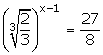
Solution 2:

3.Solve:

(i) 4^{x - 2} - 2^{x + 1} = 0

(ii)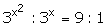 

Solution 3:

4.Solve :

(i) 8 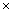2^2x + 4 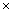2^x+1 = 1 + 2^x

(ii)2^2x + 2^x+2 - 4 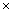2³ = 0

(iii)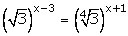 

Solution 4:

5.Find the values of m and n if:


Solution 5:

6.


Solution 6:

7.Prove that:

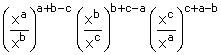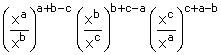(i) ₌₁

 (ii)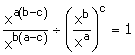 

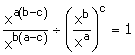
Solution 7:

8.If a^x = b, b^y = c and c^z = a, prove that: xyz = 1.

Solution 8:

9.If a^x = b^y = c^z and b² = ac, prove that :.

Solution 9:

10.If 5^-P = 4^-q = 20^r, show that:

  

Solution 10:

11.If m ≠ n and (m + n)^-1 (m^-1 + n^-1) = m^xn^y, show that:

x + y + 2 = 0

Solution 11:

12.If 5^{x + 1} = 25^{x - 2}, find the value of

3^{x - 3} × 2^{3 - x}

Solution 12:

13.If 4^{x + 3} = 112 + 8 × 4^x, find the value of (18x)^3x.

Solution 13:

14.(i)Solve for x:

 4^x-1 × (0.5)^{3 - 2x} = 

Solution 14(i):

14.(ii)Solve for x:

(a^{3x + 5})². (a^x)⁴ = a^{8x + 12}

Solution 14(ii):

14.(iii)Solve for x:

  

Solution 14(iii):

14.(iv)Solve for x:

2^{3x + 3} = 2^{3x + 1} + 48

Solution 14(iv):

14.(v)Solve for x:

3(2^x + 1) - 2^{x + 2} + 5 = 0

Solution 14(v):

Exercise 7(C)

1.


Solution 1:

2.



Solution 2:

3.Solve: 3^x-1× 5^2y-3 = 225.

Solution 3:

4.


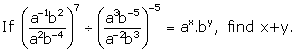
Solution 4:

5.If 3^x+1 = 9^x-3, find the value of 2^1+x.


Solution 5:

6.


Solution 6:

7.

Solution 7:

8.



Solution 8:

9.


Solution 9:

10.Solve: 3(2^x + 1) - 2^x+2 + 5 = 0.

Solution 10:

11.If (a^m)ⁿ = a^m .aⁿ, find the value of:

m(n - 1) - (n - 1)

Solution 11:

12.


Solution 12:

Selina Concise Mathematics Class 9 ICSE Solutions Chapter 7- Indices (Exponents)