Selina Concise Mathematics Class 9 ICSE Solutions Mean and Median
Selina ICSE Solutions for Class 9 Maths Chapter 19 Mean and Median (For Ungrouped Data Only)
Exercise 19(A)1.Find the mean of 43, 51, 50, 57 and 54.
Solution 1:
2.Find the mean of first six natural numbers.
Solution 2:
3.Find the mean of first ten odd natural number.
Solution 3:
4.Find the mean of all factors of 10.
Solution 4:
5.Find the mean of x + 3, x + 5, x + 7, x + 9 and x + 11.
Solution 5:
6.If different values of variable x are 9.8, 5.4, 3.7, 1.7, 1.8, 2.6, 2.8, 8.6, 10.5 and 11.1; find
(i) the mean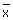 
(ii) the value of 
(ii) the value of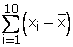 Solution 6:
7.The mean of 15 observations is 32. Find the resulting mean, if each observation is :
(i) Increased by 3
(ii) Decreased by 7
(iii) Multiplied by 2
(iv) Divided by 0.5
(v) Increased by 60%
(vi) Decreased by 20%
Solution 7:
8.The mean of 5 numbers is 18. If one number is excluded, the mean of remaining number becomes 16. Find the excluded number.
Solution 8:
9.If the mean of observations x, x + 2, x + 4, x + 6 and x + 8 is 11, find:
(i) The value of x;
(ii) The mean of first three observations.
Solution 9:
10.The mean of 100 observations is 40. It is found that an observation 53 was misread as 83. Find the correct mean.
Solution 10:
11.The mean of 200 items was 50. Later on, it was discovered that two items were misread as 92 and 8 instead of 192 and 88. Find the correct mean.
Solution 11:
12.Find the mean of 75 numbers, if the mean of 45 of them is 18 and the mean of the remaining ones is 13.
Solution 12:
13.The mean weight of 120 students of a school is 52.75 kg. If the mean weight of 50 of them is 51 kg, find the mean weight of the remaining students.
Solution 13:
14.The mean marks (out of 100) of boys and girls in an examination are 70 and 73 respectively. If the mean marks of all the students in that examination is 71, find the ratio of the number of boys to the number of girls.
Solution 14:
Exercise 19(B)
1.Find the median of:
(i) 25, 16, 26, 16, 32, 31, 19, 28 and 35
(ii) 241, 243, 347, 350, 327, 299, 261, 292, 271, 258 and 257
(iii) 63, 17, 50, 9, 25, 43, 21, 50, 14 and 34
(iv) 233, 173, 189, 208, 194, 204, 194, 185, 200 and 220.
Solution 1:
2.The following data have been arranged in ascending order. If their median is 63, find the value of x.
34, 37, 53, 55, x, x + 2, 77, 83, 89 and 100.
Solution 2:
3.In 10 numbers, arranged in increasing order, the 7th number is increased by 8, how much will the median be changed?
Solution 3:
4.Out of 10 students, who appeared in a test, three secured less than 30 marks and 3 secured more than 75 marks. The marks secured by the remaining 4 students are 35, 48, 66 and 40. Find the median score of the whole group.
Solution 4:
5.The median of observations 10, 11, 13, 17, x + 5, 20, 22, 24 and 53 (arranged in ascending order) is 18; find the value of x.
Solution 5:
Exercise 19(C)
1.Find the mean of 8, 12, 16, 22, 10 and 4. Find the resulting mean, if each of the observations, given above, be:
(i) multiplied by 3.
(ii) divided by 2.
(iii) multiplied by 3 and then divided by 2.
(iv) increased by 25%
(v) decreased by 40%
Solution 1:
2.The mean of 18, 24, 15, 2x + 1 and 12 is 21. Find the value of x.
Solution 2:
3.The mean of 6 numbers is 42. If one number is excluded, the mean of remaining number is 45. Find the excluded number.
Solution 3:
4.The mean of 10 numbers is 24. If one more number is included, the new mean is 25. Find the included number.
Solution 4:
5.The following observations have been arranged in ascending order. If the median of the data is 78, find the value of x.
44, 47, 63, 65, x + 13, 87, 93, 99, 110.
Solution 5:
6.The following observations have been arranged in ascending order. If the median of these observations is 58, find the value of x.
24, 27, 43, 48, x - 1, x + 3, 68, 73, 80, 90.
Solution 6:
7.Find the mean of the following data:
30, 32, 24, 34, 26, 28, 30, 35, 33, 25
(i) Show that the sum of the deviations of all the given observation from the mean is zero.
(ii) Find the median of the given data.
Solution 7:
8.Find the mean and median of the data:
35, 48, 92, 76, 64, 52, 51, 63 and 71.
If 51 is replaced by 66, what will be the new median?
Solution 8:
9.The mean of x, x + 2, x + 4, x + 6 and x + 8 is 11, find the mean of the first three observations.
Solution 9:
10.Find the mean and median of all the positive factors of 72.
Solution 10:
Selina Concise Mathematics Class 9 ICSE Maths Solutions Chapter 19 - Mean and Median