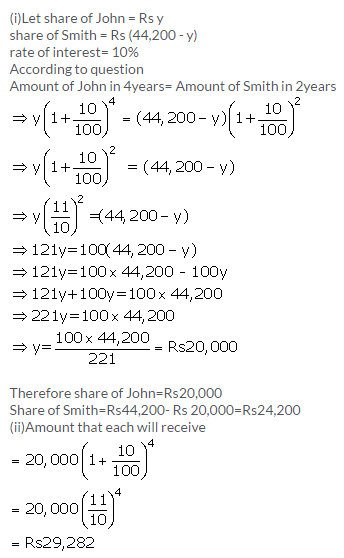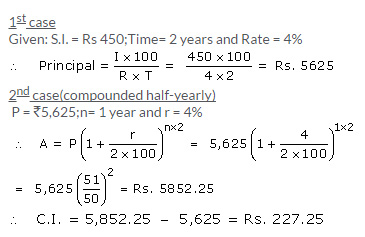Selina Concise Mathematics Class 9 ICSE Solutions Compound Interest (Using Formula)
Selina ICSE Solutions for Class 9 Maths Chapter 3 Compound Interest (Using Formula)
Exercise 3(A)
1. Find the amount and the compound interest on Rs. 12,000 in 3 years at 5% compounded annually.
Solution 1:
2. Calculate the amount of Rs.15,000 is lent at compound interest for 2 years and the rates for the successive years are 8% and 10% respectively.
Solution 2:
3. Calculate the compound interest accrued on Rs.6,000 in 3 years, compounded yearly, if the rates for the successive years are 5%, 8% and 10% respectively.
Solution 3:
4. What sum of money will amount to Rs. 5,445 in 2 years at 10% per annum compound interest?
Solution 4:
Solution 5:
6. Find the sum on which the compound interest for 3 years at 10% per annum amounts to Rs.1,655.
Solution 6:
7. What principal will amount to Rs. 9,856 in two years, if the rates of interest for successive years are 10% and 12% respectively?
Solution 7:
8. On a certain sum, the compound interest in 2 years amounts to Rs.4,240. If the rate of interest for the successive years is 10% and 15% respectively, find the sum.
Solution 8:
9. At what per cent per annum will Rs.6,000 amount to Rs.6,615 in 2 years when interest is compounded annually?
Solution 9:
At 5% per annum the sum of Rs.6,000 amounts to Rs.6,615 in 2 years when the interest is compounded annually.
10. At what rate per cent compound interest, does a sum of money become 1.44 times of itself in 2 years?
Solution 10:
Let Rs.x and Rs.y be the money invested by Pramod and Rohit respectively such that they will get the same sum on attaining the age of 25 years.
Pramod will attain the age of 25 years after 25 – 16 = 9 years
Rohit will attain the age of 25 years after 25 -18 = 7 years
Pramod and Rohit should invest in 400:441 ratio respectively such that they will get the same sum on attaining the age of 25 years.
11. At what rate per cent will a sum of Rs. 4,000 yield Rs. 1,324 as compound interest in 3 years?
Solution 11:
12. A person invests Rs.5,000 for three years at a certain rate of interest compounded annually. At the end of two years this sum amounts to Rs.6,272. Calculate :
(i) the rate of interest per annum.
(ii) the amount at the end of the third year.
Solution 12:
13. In how many years will Rs.7,000 amount to Rs.9,317 at 10% per annum compound interest?
Solution 13:
14. Find the time, in years, in which Rs.4,000 will produce Rs,630.50 as compound interest at 5% compounded annually.
Solution 14:
15. Divide Rs.28,730 between A and B so that when their shares are lent out at 10% compound interest compounded per year, the amount that A receives in 3 years is the same as what B receives in 5 years.
Solution 15:
16. A sum of Rs. 44,200 is divided between John and Smith, 12 years and 14 years old respectively, in such a way that if their portions be invested at 10% per annum compound interest, they will receive equal amounts on reaching 16 years of age.
(i) What is the share of each out of Rs.44,200?
(ii) What will each receive, when 16 years old?
Solution 16:
17. The simple interest on a certain sum of money and at 10% per annum is Rs. 6,000 in 2 years, Find:
i. the sum.
ii. the amount due to the end of 3 years and at the same rate of interest compounded annually.
iii. the compound interest earned in 3 years.
Solution 17:
18. Find the difference between compound interest and simple interest on Rs. 8,000 in 2 years and at 5% per annum.
Solution 18:
Exercise 3(B)
1. The difference between simple interest and compound interest on a certain sum is Rs. 54.40 for 2 years at 8 per cent per annum. Find the sum.
Solution 1:
2. A sum of money, invested at compound interest, amounts to Rs. 19, 360 in 2 years and to Rs.23,425.60 in 4 years. Find the rate percent and the original sum of money.
Solution 2:
3. A sum of money lent out at C.I. at a certain rate per annum becomes three times of itself in 8 years. Find in how many years will the money becomes twenty-seven times of itself at the same rate of interest p.a.
Solution 3:
4. On what sum of money will compound interest (payable annually) for 2 years be the same as simple interest on
9,430 for 10 years, both at the rate of 5 per cent per annum?Solution 4:
5. Kamal and Anand each lent the same sum of money for 2 years at 5% at simple interest and compound interest respectively. Anand received
15 more than Kamal. Find the amount of money lent by each and the interest received.Solution 5:
For kamal, interest = 
For Anand, interest =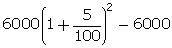 
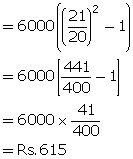
6. Simple interest on a sum of money for 2 years at 4% is
450. Find compound interest of the same sum and at the same rate for 2 yearsSolution 6:
7. Simple interest on a certain sum of money for 4 years at 4% per annum exceeds the compound interest on the same sum for 3 years at 5 per cent per annum by
228. Find the sum.Solution 7:
8. Compound interest on a certain sum of money at 5% per annum for two years is Rs.246. Calculate simple interest on the same sum for 3 years at 6% per annum.
Solution 8:
9. A certain sum of money amounts to Rs. 23,400 in 3 years at 10% per annum simple interest. Find the amount of the same sum in 2 years and at 10% p.a. compound interest.
Solution 9:
10. Mohit borrowed a certain sum at 5% per annum compound interest and cleared this loan by paying Rs. 12,600 at the end of the first year and Rs. 17,640 at the end of the second year. Find the sum borrowed.
Solution 10:
Exercise 3(C)
1. If the interest is compounded half-yearly, calculate the amount when principal is Rs.7,400; the rate of interest is 5% per annum and the duration is one year.
Solution 1:
2. Find the difference between the compound interest compounded yearly and half-yearly on Rs10,000 for 18 months at 10% per annum.
Solution 2:
3. A man borrowed Rs.16,000 for 3 years under the following terms:
20% simple interest for the first 2 years.
20% C.I. for the remaining one year on the amount due after 2 years, the interest being compounded half-yearly.
Find the total amount to be paid at the end of the three years.
Solution 3:
4. What sum of money will amount to Rs.27,783 in one and a half years at 10% per annum compounded half yearly?
Solution 4:
5. Ashok invests a certain sum of money at 20% per annum, compounded yearly. Geeta invests an equal amount of money at the same rate of interest per annum compounded half-yearly. If Geeta gets Rs33 more than Ashok in 18 months, calculate the money invested.
Solution 5:
6. At what rate of interest per annum will a sum of Rs.62,500 earn a compound interest of Rs.5,100 in one year? The interest is to be compounded half yearly.
Solution 6:
7. In what time will Rs.1,500 yield Rs.496.50 as compound interest at 20% per year compounded half-yearly?
Solution 7:
8. Calculate the C.I. on Rs.3,500 at 6% per annum for 3years, the interest being compounded half-yearly.
Do not use mathematical tables. Use the necessary information from the following:
(1.06)3 =1.191016; (1.03)3 = 1.092727
(1.06)6 =1.418519; (1.03)6 = 1.194052
Solution 8:
9. Find the difference between compound interest and simple interest on Rs12,000 and in
years at 10% compounded yearly.Solution 9:
10. Find the difference between compound interest and simple interest on Rs12,000 and in
years at 10% compounded half-yearly.Solution 10:
Exercise 3(D)
1. The cost of a machine is supposed to depreciate each year at 12% of its value at the beginning of the year. If the machine is valued at Rs44,000 at the beginning of 2008, find its value :
(i) at the end of 2009.
(ii) at the beginning of 2007.
Solution 1:
2. The value of an article decreases for two years at the rate of 10% per year and then in the third year it increases by 10%. Find the original value of the article, if its value at the end of 3 years is Rs.40,095.
Solution 2:
3. According to a census taken towards the end of the year 2009, the population of a rural town was found to be 64,000. The census authority also found that the population of this particular town had a growth of 5% per annum. In how many years after 2009 did the population of this town reach 74,088 ?
Solution 3:
4. The population of a town decreased by 12% during 1998 and then increased by 8% during 1999. Find the population of the town, at the beginning of 1998, if at the end of 1999 its population was 2,85,120.
Solution 4:
5. A sum of money, invested at compound interest, amounts to Rs 16,500 in 1 year and to Rs.19,965 in 3 years. Find the rate per cent and the original sum of money invested.
Solution 5:
6. The difference between C.I. and S.I. on Rs.7,500 for two years is Rs.12 at the same rate of interest per annum. Find the rate of interest.
Solution 6:
7. A sum of money lent out at C.I. at a certain rate per annum becomes three times of itself in 10 years. Find in how many years will the money become twenty-seven times of itself at the same rate of interest p.a.
Solution 7:
8. Mr. Sharma borrowed a certain sum of money at 10% per annum compounded annually. If by paying Rs.19,360 at the end of the second year and Rs.31,944 at the end of the third year he clears the debt; find the sum borrowed by him.
Solution 8:
9. The difference between compound interest for a year payable half-yearly and simple interest on a certain sum of money lent out at 10% for a year is Rs.15. Find the sum of money lent out.
Solution 9:
10. The ages of Pramod and Rohit are 16 years and 18 years respectively. In what ratio must they invest money at 5% p.a. compounded yearly so that both get the same sum on attaining the age of 25 years?
Solution 10:
Exercise 3(E)
1. Simple interest on a sum of money for 2 years at 4% is Rs.450. Find compound interest on the same sum and at the same rate for 1 year, if the interest is reckoned half yearly.
Solution 1:
2.
Solution 2:
3. The value of a machine, purchased two years ago, depreciates at the annual rate of 10%. If its present value is Rs.97,200, find:
i. Its value after 2 years.
ii. Its value when it was purchased.
Solution 3:
4. Anuj and Rajesh each lent the same sum of money for 2 years at 8% simple interest and compound interest respectively. Rajesh received Rs.64 more than Anuj. Find the money lent by each and interest received.
Solution 4:
5. Calculate the sum of money on which the compound interest (payable annually) for 2 years be four times the simple interest on Rs.4,715 for 5 years, both at the rate of 5% per annum.
Solution 5:
6. A sum of money was invested for 3 years, interest being compounded annually. The rates for successive years were 10%, 15% and 18% respectively. If the compound interest for the second year amounted to Rs.4,950, find the sum invested.
Solution 6:
7. A sum of money is invested at 10% per annum compounded half yearly. If the difference of amounts at the end of 6 months and 12 months is Rs.189, find the sum of money invested.
Solution 7:
8. Rohit borrows Rs.86,000 from Arun for two years at 5% per annum simple interest. He immediately lends out this money to Akshay at 5% compound interest compounded annually for the same period. Calculate Rohit's profit in the transaction at the end of two years.
Solution 8:
9. The simple interest on a certain sum of money for 3 years at 5% per annum is Rs.1,200. Find the amount and the compound interest due on this sum of money at the same rate and after 2 years. Interest is reckoned annually.
Solution 9:
10. Nikita invests Rs.6,000 for two years at a certain rate of interest compounded annually. At the end of first year it amounts to Rs.6,720. Calculate:
(a) The rate of interest.
(b) The amount at the end of the second year.
Solution 10:
