Selina Concise Mathematics Class 9 ICSE Solutions Triangles [Congruency in Triangles]
Selina ICSE Solutions for Class 9 Maths Chapter 9 Triangles [Congruency in Triangles]
Exercise 9(A)1.Which of the following pairs of triangles are congruent? In each case, state the condition of congruency:
(a) In  ABC and
ABC and  DEF, AB = DE, BC = EF and
DEF, AB = DE, BC = EF and  B =
B =  E.
E.
(b) In  ABC and
ABC and  DEF,
DEF,  B =
B =  E = 90o; AC = DF and BC = EF.
E = 90o; AC = DF and BC = EF.
(c) In  ABC and
ABC and  QRP, AB = QR,
QRP, AB = QR,  B =
B =  R and
R and  C = P.
C = P.
(d) In  ABC and
ABC and  PQR, AB = PQ, AC = PR and BC = QR.
PQR, AB = PQ, AC = PR and BC = QR.
(e) In  ADC and
ADC and  PQR, BC = QR,
PQR, BC = QR,  A = 90o,
A = 90o,  C =
C =  R = 40o and
R = 40o and  Q = 50o.
Q = 50o.
Solution 1:
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://images.topperlearning.com/topper/bookquestions/201923_image064.jpg)
Show that OP is perpendicular to AB.
Solution 2:
3.The following figure shows a circle with centre O.
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://images.topperlearning.com/topper/bookquestions/201925_image072.jpg)
If OP is perpendicular to AB, prove that AP = BP.
Solution 3:
4.In a triangle ABC, D is mid-point of BC; AD is produced upto E so that DE = AD. Prove that:
(i)  ABD and
ABD and  ECD are congruent.
ECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC.
Solution 4:
5.A triangle ABC has
Prove that:
(i) The perpendiculars from the mid-point of BC to AB and AC are equal.
(ii) The perpendiculars form B and C to the opposite sides are equal.
Solution 5:
6.The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
Solution 6:
7.A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that: QA = QB.
Solution 7:
8.If AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
Solution 8:
9.From the given diagram, in which ABCD is a parallelogram, ABL is al line segment and E is mid point of BC.
Prove that:
(i)  DCE
DCE 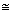
 LBE
LBE
(ii) AB = BL.
(iii) AL = 2DC
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://images.topperlearning.com/topper/bookquestions/201937_image126.jpg)
Solution 9:
10.In the given figure, AB = DB and Ac = DC.
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Solutions Icse Class 9 Mathematics Chapter - Triangles Congruency In Triangles](https://images.topperlearning.com/topper/bookquestions/201939_image134.jpg)
If 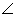 ABD = 58o,
ABD = 58o,
Solution 10:
11.In the given figure: AB//FD, AC//GE and BD = CE; prove that:
(i) BG = DF
(ii) CF = EG
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Solutions Icse Class 9 Mathematics Chapter - Triangles Congruency In Triangles](https://images.topperlearning.com/topper/question_uploads/ICSE_IX_chap13_Ex13(A)_SHR_files/20140924134305_image001.jpg)
Solution 11:
12.In ∆ABC, AB = AC. Show that the altitude AD is median also.
Solution 12:
13.In the following figure, BL = CM.
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Solutions Icse Class 9 Mathematics Chapter - Triangles Congruency In Triangles](https://images.topperlearning.com/topper/question_uploads/ICSE_IX_Maths_CongruenceofTriangles_files/20160715191049_image009.png)
Prove that AD is a median of triangle ABC.
Solution 13:
14.In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that :
(i) BD = CD
(ii) ED = EF
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Solutions Icse Class 9 Mathematics Chapter - Triangles Congruency In Triangles](https://images.topperlearning.com/topper/question_uploads/ICSE_IX_Maths_CongruenceofTriangles_files/20160715191049_image013.png)
Solution 14:
15.Use the information in the given figure to prove :
(i) AB = FE
(ii) BD = CF
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Solutions Icse Class 9 Mathematics Chapter - Triangles Congruency In Triangles](https://images.topperlearning.com/topper/question_uploads/ICSE_IX_Maths_CongruenceofTriangles_files/20160715191049_image017.png)
Solution 15:
16.
Solution 16:
Exercise 9(B)
1.On the sides AB and AC of triangle ABC, equilateral triangle ABD and ACE are drawn.
Prove that: (i) 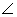 CAD =
CAD = 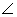 BAE (ii) CD = BE.
BAE (ii) CD = BE.
Solution 1:
2.In the following diagrams, ABCD is a square and APB is an equilateral triangle.
In each case,
(i) Prove that:  APD
APD 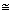
 BPC
BPC
(ii) Find the angles of  DPC.
DPC.
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Solutions Icse Class 9 Mathematics Chapter - Triangles Congruency In Triangles](https://images.topperlearning.com/topper/bookquestions/201993_image025.jpg)
Solution 2:
3.In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. Prove that:
(i)  ACQ and
ACQ and  ASB are congruent.
ASB are congruent.
(ii) CQ = BS.
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Solutions Icse Class 9 Mathematics Chapter - Triangles Congruency In Triangles](https://images.topperlearning.com/topper/bookquestions/201995_image064.jpg)
Solution 3:
4.In a
Solution 4:
5.In the adjoining figure, OX and RX are the bisectors of the angles Q and R respectively of the triangle PQR.
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Solutions Icse Class 9 Mathematics Chapter - Triangles Congruency In Triangles](https://images.topperlearning.com/topper/bookquestions/201999_image087.jpg)
If XS 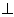 QR and XT
QR and XT 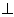 PQ ; prove that:
PQ ; prove that:
(i) 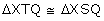
(ii) PX bisects angle P.
Solution 5:
6.In the parallelogram ABCD, the angles A and C are obtuse. Points X and Y are taken on the diagonal BD such that the angles XAD and YCB are right angles.
Prove that: XA = YC.
Solution 6:
7.ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such produced to E and F respectively, such that AB = BE and AD = DF.
Prove that:
Solution 7:
8.In the following figures, the sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and median PS of the triangle PQR. Prove that
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Solutions Icse Class 9 Mathematics Chapter - Triangles Congruency In Triangles](https://images.topperlearning.com/topper/bookquestions/202005_image129.jpg)
Solution 8:
9.In the following diagram, AP and BQ are equal and parallel to each other.
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Solutions Icse Class 9 Mathematics Chapter - Triangles Congruency In Triangles](https://images.topperlearning.com/topper/bookquestions/202013_image161.jpg)
Prove that:
(i) ![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Solutions Icse Class 9 Mathematics Chapter - Triangles Congruency In Triangles](https://images.topperlearning.com/topper/bookquestions/202013_image163.gif)
(ii) AB and PQ bisect each other.
Solution 9:
10.In the following figure, OA = OC and AB = BC.
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Solutions Icse Class 9 Mathematics Chapter - Triangles Congruency In Triangles](https://images.topperlearning.com/topper/bookquestions/202015_image169.jpg)
Prove that:
(i) 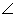 AOB = 90o
AOB = 90o
(ii)  AOD
AOD 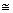
 COD
COD
(iii) AD = CD
Solution 10:
11.The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that:
(i) AM = AN (ii)  AMC
AMC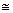
 ANB
ANB
(iii) BN = CM (iv)  BMC
BMC 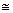
 CNB
CNB
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Solutions Icse Class 9 Mathematics Chapter - Triangles Congruency In Triangles](https://images.topperlearning.com/topper/bookquestions/202017_image185.jpg)
Solution 11:
12.In a triangle ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that : AD = CE.
Solution 12:
13.PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL= MR. Show that LM and QS bisect each other.
Solution 13:
14.In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced upto point R so that CR = BP.
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Solutions Icse Class 9 Mathematics Chapter - Triangles Congruency In Triangles](https://images.topperlearning.com/topper/question_uploads/ICSE_IX_Maths_CongruenceofTriangles_files/20160715191049_image048.png)
Prove that QR bisects PC.
Hint: (Show that ∆ QBP is equilateral
⇒ BP = PQ, but BP = CR
⇒ PQ = CR ⇒ ∆ QPM ≅ ∆ RCM)
Solution 14:
15.
Solution 15:
16.
Solution 16:
17.
18.
Solution 18:
19.
Solution 19:
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgZmiKLREqeMxfVboAOuCZN3-abk0x17d54IbMBpVP7-OlxaQA3FPSSfbxpimT9bkdyvLI4PcsG8z04ZpL4TnR7p-DWca6VBpYtd3tSkoBmBsC3Qg2ZebvZ5ikJRN3B3k5uAqLTA0ZuH8Cj/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEitEams4ptNBQ4dZg3TM5xW654NJWUEnDcYhfipt0ivs3XdQNaVLbBG8b5bpEFBXRwXw2d0J2HfXVN7mzm6XeprArbPIcp8ft0OfFVekmumb5c8KDtjU9wA0HQu7Y5lozpzgoOAMXSPVcdH/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles1.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgOK-yI-J2aXHxUArJrMscfqxnavN8faEKnI-8J4Ndqx4EIbotLq45nun6ei722yPXiaumgjTHpUkIZnKUpx5CfUd8YYX5hpgCQ26ndtxqgaPR1606D9e7aeTWmbQzzdM8XakyCUPAICA2v/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles2.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgZFD2fLuUAUxq74fRHVpX9CA1mPq_cyREQTZEzcEgR8QWlK_uM5NtaC_yPaMME6KjpvwW7mro7iyKXrsg-zpCZd7_pdTcDp2ZCO6xKRR3UCiEdWe5EEqIrfFLfC0HZ40vqT7ZGhs0itUz2/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles3.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEii1-2tHtWzFw7nKd1112VmbOFjHGYDGepLm3doEXbIZNOni4napcyyPlyoR2K1tQwjZfvlOly4Vb8U4BG9oc6FHZZh7t517rOSJffgK0MbNuT_7OPrtDJTXXpjXt2NpsfTBxUXkm-pr_nm/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles4.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgeewzLJcz1jLmoLJsl4AWuERi1ahOklQmFOqRQNQ9As2savF3wkDnxZPOjZW-EHddRpcd2UC7wpaZUSOgbth3i7xTg5qAPzZuIaM4XGfQL3Ys5pBvxMrituYGyYP_rp0RT0evRJ_GdhacV/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles5.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhSK4wCeX5qW2jVcrpCtDz3aQiY91aflGcX7_icilKV9vI8OQvNqsVnS93GnVQn8BvxHnV_YH22jMsmmE-nrWhQHWxtCuDw54LVrSHmx8cCHcp6P7HGOLTh-uotlQxhCUT7AtjYP3lvmyDN/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles6.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgOMwPt0_OkGGXZmqXBX-o_JxeHeMptTuV-leUDR6BuqpTx0JkH-Kw9xBgsvh65JkTdAtepvJnNTYoJhLkfevH2L4ytGy1f_k4-5ayhcEp5uSH5FSxyKhU8qMUOxoHf83GNNP2AACf8fRDz/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles7.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhoWN7lxetW06FJNm18LQMHbJ6v-hycIVj_Gka3mxi4-zaRg1n9NIG4N3izmpKVDr3QdGrb7TZkHwuHOKKfaRQ5-bLFM4gzbtSpKQJYZepMnkj1eP3D23Scw_s53Y8GAYhVyPXCb7HwRNjt/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles8.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiwSpuCbyoiIoJoG8Cq1Nm1Ub2iIQJBWWo_3MZF3-K__BXK2FVkmcmGBawUp-0mKFHjg3aN7h_bqZ9Sm-CHi3fk-F4bgRGrKvXPvlUpv0CxDJc-W0EQrXH1BsCiX3ou7A7uo3pFL6Dst0Pj/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles9.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiFkO-4ZObZ7EFlWP0GMa-WRA7ZJRD-q8nDjyr0aS2uQk1EE3o4BqRk86tfVOrHCzRuDlwfNU4tIfIkGikuP0HcmlrGuqroai2-5pBXGVfYtFqyV6KMQhqF_c9MHxD-An0-HnIW9o1wTJbL/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles10.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhYLeTp3uVjUrzophq7NALssX-CpNVpcvNw3Hb9eyBwAINWuAglbxr7CJ_XojiBPVeizFzKzMUw9SV8ePMl5qPq4ziWiOvGj7wZl9oEemxlI1vb8iIwOzZlJjVHX1ThSCsK1eD_eYEmEwHY/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles11.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhYjOlCT2RF1QMUBiBn82Tyz-ITfquRjeAIDlFo-XZc_SDRAbYKsfqUsT5Y1j0_VxEAjr1jRVuVhkq-_xZepE1ayAlrmRxhlkNzl1xs6740wMPg2GXJqSWG2G_W-P0srZ0IQFf2HdRU3K9K/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles12.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjs803P4uBGer_0uYEwTaVtAFKJjWl7YJ4gzl8W4Q7Lj-og7Mk9YzP-C9n62lPQaZXJr3tS99Szq7pOykqma2D-69cJwApaUqaYiAWH9LRnEV29l1csZXDP0lJY348kHkvn2-n79rx78NKe/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles13.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiCWxCtHQKwebrWzQxgZf-Vtnj9WNMJHQxNu-KChUDKhJfChqGgbUYA6o4ANd-l4mkmyFcpI0IJ0c-5VrDixJKxMCvYEXCk975CNB0mH5qjU8IdoqO0Iry-L8_Wm2HUDvCH-9zCFeVJhEaQ/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles14.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiykyMP4-YQ2bfGRnzZwltRz2PjjDctV6pGa_CflFmi2Ej_mHLkVGclh3Qj_Sn-N6sRYpMuBCLBLzNctCXy-0Ggk0QFSqTyShARZYfMJ7KhotXRPTje3dnaygoiF8qKX-YwfYZqxa1RjBqQ/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles15.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjV3ZKohKO0mIRcEWBqTnY-_kAkdRf-VN6Fw76MHONNHJ-l-Hk5F60O7MTQtpWuZ2CkWhPw_xGSfZXg6EGmzZvgXSoyghOshwM32APkI5m2cvQ4sGH6jLv_7qD6D-r4iwPJ6gW4sZIjj8rf/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles16.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjHEFmXIwaYxKPNVeFEzw8rjQKG7cqVHEH4s14zQhI1GDGlhigmtQmQaVvcGTX23jOQiKXBwJNg-92aa3BfpM9ogVufFiHx1on22Wc8t-geOimyzdkU2zmT_n3zZaMS6rEdRSdoUXvFhWxj/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles17.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj4Itq1A5E4f9J7TKaU4h4sK54WbfBY81hCUSOBweFGPuDqURylTFUb6_94SNSD-PXDDPRNOtEsuzhBULY8NzlGdrwCs04ohQ5qlSjJhmaxehmXfZ_RyJ0R8S9yC7I1CxBmciV-3I4khfT0/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles18.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhw6XRGOJ7ig_uhLvUu9VS5Jp2IxFubSulwIWbajBeWuw0gNdVYAmDEUjdZhziB7IfSKqPRXwPsAzdOVuSHU8GpG8NPRn-fAQj1ddnh6hyphenhyphenmOCu3lt0p1ojP6RuZ1VqRwEDaKpBW_874crEx/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles19.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhSCYPbxLEgGL69RIzg3D8KLez69qeUAIDK3oM_U7kxbfEzZoPR30JcS_Dl8vJA3YE2dTo-N8cxHDCdEp-eRdI3SRgXiP0OH0JrX-ZJGCAntLegGL6gh4IPbJXktlp0nzJzuQdZ05fbB7R3/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles21.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhOLcfjRfj-9lEypWLp2A-UCGA0CMzTQU2ehEBx6fOM1z-un-JO_AqAi94MTdRO65oyJbZ3m5A7njhj6cPi5DPsLPXPiMdhCZUnx6bUs4_KKH_gwePY_pkMy1r7Jeh_hQUsCT6Hmt6XIihk/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles22.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjwzslfxng-8DzrHEo0isXRUBZ4Bh8GqeB9D6CT7fscI-VQ9SI-NAyvyA7zWEjcEftG7erAGgCT8Fw3oHiHFygQ-m4IRUKDYhOOX9JEKGvoaWY5BgPpf_EplIkBmCkgU6yloKcraiNiibic/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles23.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjSZJPkF6-UDvUGAN8ovpWpp7DDfPvo7oD4Zqr3eSdDa0pqWIF2x0OaTHw47bj0WyByl0R3drtpNx54aX0m60gMa9dPZcjmu0cADPoD6GN4k35I1VooYNy03_d5YXR8wT9Z4KOHP9Ct5u0a/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles24.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh8yrWknf7UTuZMfbXjQCHMC5Evj5iDZ9hZU3-qH4emY_N9ABpsXWHdR6VPTTrKYJUyf7chKZ632ZoJ_aVXm-se7_J5BjzowhdKbsb7KKqHFYh2RFvg335esWzq_kc0I_1AHlCNj7xpgq6M/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles25.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEglz3cXYOuAhm908w26mhgdX3HoK0QfIcBRklxKM1W8v1lAqhp7x8ahhjfVL2oqgn6U9WtHb7dcch32QV-ejYg18iy6MT0GrSIzOqYqxrzd96KhjLevInwR6tSvR7WGEDG0YXij4McJwJKl/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles26.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh_oXFcol9UHoRfpt8aR9cJhrjpktzFvE-efvX1YVVxcELHSq1e540YSZPjni6Nl9U_qPVLEza4NPAGd-5cr_8NjqbN_jfyZnyvv26agzLgHFTaDHHlyxnjJeRPF9O8c6pu5Nui4DB3omd7/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles27.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgYYzMtQacjICmQ4KE_4OJWCzkdh4upadp0kszgHvQri_SQCm_HhnzRI6BWU3-3L8BYNvmuGuh3JEPJAhwJHVkKrNKklXUuK_I-hJm9p16xef-6AN6wzHJpxl9wT-_D_xZ2dAqq_xbLbjKo/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles28.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhw3VddlgqfXsI6KBcAqGW7B8c2BcfyzttoO46Inj2F-gUqMiYFbsHuhiY_Pm2EWnKox0j8rMl6Yv7265D_pmuEIQK68IDonc_rhwcTfhzd4u3bnQchQtebPJa06pCz9bb2Ab1BsS7s02S_/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles29.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhjxGo9yF-Ot_c2HdvwHxALduVcHi60BE96rUqalS2qXZAdktN2LYaowcf0pB2fx66xFlawR26TmG9m4XUMIEjwns3zbWIkjR9smsLn-yzQcoGmcsCnG5EI2SlFnlTS6UB2O0j4OXOlzMLt/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles30.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjKR7DSyC73QvjF_3x4kP_PhatpT5WIcUlzeL6MHKNZiBABcleIvm4JtNTYujmZHWFkPCk5NATfdlmcy95d-z4Rz_nKlBCA2zsbpWtV5EuV22U4WpA6JcTzmLW_X-GKCaJoJvDM9MgbaxjJ/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles31.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhUXsT4sLmAU5QnTiN7U0TPrLOhcX2e7P4nAQmZ-OKjaqnnuyo0sWXqvPbZ9a11MVifAc7Z3U5JXjv5qQW38zZO6B2LNSWEKlt0-CpL9h0f9_UQt8ZMIKSm3mNEOXT4qy0uCZXKguM5PgDV/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles32.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg9fuPnHOuF00slLRivibiBrh9ryTrPc3gZb0DxT4O-sPCuh5E-Mvwt9SxrWRuS992aK250LdctHhnQSntcnjfxNuN-MeTL6BqgFrvGAg1zRQhU84Uk6fsa5Pf_QuhuroxNk9WEsfl2Bveh/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles33.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEie0hQ5kmEshH6kA0dC66czuk1e2J6INVVLIAKftsxdKAcRDU3JPLnxl3zDFlQpBfg-EmWmEBXAj561J7dSeOjqebRDCd2XWktEmk-lX65XPROzCAMzEHelW0OCJ_29vzendUucdtI1FOLE/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles34.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhy7MeGebyEW5wi_I87GEEQF8V3SuW7rDlInfPhqAQpSUw7fWTACErf3D6aDb2GpKaRSXPgSLgg6fkTEkmTIUgvtIHtuGQFr3HqfuyP9FqK78dNZC2DtKBNTmaxPeTJ7k3X3CUhswynSn84/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles35.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhVS8Z1LzPhRhgMyF7SPZS8CussZ76pV4oej8dHDMJ82DytTzTlNS5pGBRnQRrvCf-OV8tWfz1nMfPq5XxyhuqGp3tyxWe2I7eeHyFNzHRYDcpOZrvqTJm6xydTq5slPP-6iVifTx8wpS3P/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles36.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh7DqMfI9sdu1D6FBlTRLlQr0G0zgNfOKw6lJ0cxsfru7cgra_837JTTPQaABJY-qPU-B15aSGn2PDcXteY7KM_faYsJ1AelCX52XS-QHmdiHq2U5sKmybQFVVzwtg3HvR0NayST1c8WL9l/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles37.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgCESDeX7zqLc3v1naZ1-CFrhNktVMFTKzZkEsw5cgItbd8v1ct5PBziQUjY5USAY8c_OmxNzWmWK705bs1TG50AWo-XyFdK3mZv8NKPrMyE9eOUVljnLUJlQcrGrV5ZAQOflKe-hldYkcj/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles38.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg_P3qFeiiRoXJYmAWwds_is9Bf9n6uYApOceMY3OK59fgpqLTpYb-NvjW1LUXBoHnUn3b-IfC6RQYW472n38rLIpHqmOFtNJfuOcrEj79VPABFIR-Xca2Jyzu30cdfg5BG_s-PHKXCs8aJ/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles39.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj2KGPqr1U8THhTwlW3wUErVJapFPnULD4axWmZ14-paggjmycB5ubxpFMGUgQab25SYDPV8SucosZfBHkUVgRZx82SmAnPLyjl0D6_D23lEDlmrbLG0FOPzO5cJgUtaCVYlG-vHY8GTWRH/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles40.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj1fZzerBkIyLq6J1P8UDIehlRBr0S6U1fP4Q5dGqtWUXW9ADP3MUUyOPGPF-q5JhihlNd2MGCxjpMnZJ_pfwKPt1hW4WjFStzcyoZp-rFBQPnI64z_Sf5x4euAIiJ0xTn2rUGy41mHJAf2/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles41.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg1kWkBtdlxuh8Kt0ryZWaAQQ9ynNOVpri96O4DEMddY6FT4qT98O6Nwlgai1t_1VaDp8k_NrEsAdh1raol2kOEIMwnHD87Hnk0L3B-RE5dmXlxs5YxfQ5KaC6YrZKTLy2NhKrGZc5Sr9bl/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles42.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjNM5OPbeqybaCui5Ejy08jD42-GanpQh6SjzvNe7mHLsoR-72moxBoQLEay-oBKBC0V2Uw8i8QYtaLTzCulTiVe_IYDiqE4taHPv-GCopGFj6RYxmr633ZH6XA8IE2QiynN-v3AE7ZAWFl/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles43.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhPyh5OVIpYgF840a73X_rhQjczKQY4DufGY9hVL4ysWkx3H-JhaHSkXAYq88_53MdZoRKTeDDu_hEoZXrdh5PvFoHX1Hk84fJ8agjZaqwSvZDoH0LIsDRPx834kSnrE0WyWNcNbot3X2lO/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles53.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhs2o4A5bFflN9ZnvE66ge5qmRPzwO3NgbSd0sOveqF4xNQYGuNzac1GT46PppTX6Y60MncSFUbWIusWb3__FWQiBnPWDW9CUpV6vy269wtbSgEKqMyJQWDo09OnT9E5bPhHkWSsWREKcwg/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles45.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEikMezFS-BGOPwZYbWuBRz58nn9JIxSIiR7MTaaeANY2bW457SAmChf4w7MdsDyLUKWBncfEbk7HMNREts2s0nJ-N2bKJafOvo0TRGlDnUVHFXsMFgwVqtav6QypBpOwbJ3vFGY1SqOgjRh/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles46.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg8nw89ft9g06ZpaQOwkxbgHLau_pvkEGJxM3Wk5d9uMOh0URVBH4k3JuXKEsRdpgoTn6nU1n9hwtowz_p9AU7sEXH_36ItgPcrW5kPA3HVxG7eLmH6PgiPmzpzd_WiYi5eFPigfRsCYF-B/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles47.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh6k-Ph8TLbqA6lFtWT1kvjOhTKaWatoh7aH5eMfkd4JtsCiTJxIFg1T1Rp33lcZLV-Rr687CSFdRLmEONh6auRxhJQ5QqL2aJOLKFeiuevrYXmMRZy9LyDl-2i9vfysO8GtjjefIZ-HWfm/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles48.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjcCUL0AtcF5xW23TKMoZHTPqYydYFPeh4gUvM3k0WSNdKwNQ9KTQftPEPtDWPzDwil1ha-6VAxc3xbQ8gljxF5aQGPuWPAwQsyHFp4g0PQoSmZdJf-M-0bLfOisXi7EbKS1-kaV6T35j42/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles49.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEilZ7pwp5LW2ChOvIeJHLo13dF-1pFTb82EEoGAchgE7BoCqyRO4h09d9GeMxKSe980-4p9Y0zwsara2jyCurJtRpVxbUp_NiGVbptM55dosekJAEmC_89_gEh0D8TMU94rJyHH2AkF8rch/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles50.jpg)
![Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles] Selina Concise Mathematics Class 9 ICSE Solutions Chapter 9 - Triangles [Congruency in Triangles]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjHJoOGkpEBFEsNuDQP_78_1U7RFShplcrNgHSTkpIAjPjg2nuISjaLMlRet8QfKJxxJdb4d2NhcibU-VU_8V93sQkSv1rN9T4_J4iH4RPQshSIZ_IApuCbdzLZbaSjypUiCEzk1gcocUyl/s1600/selina-concise-mathematics-class-9-icse-solutions-triangles-congruency-in-triangles52.jpg)