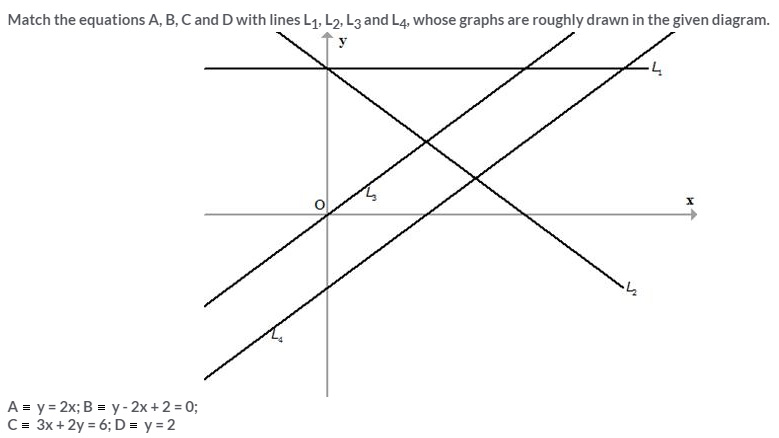
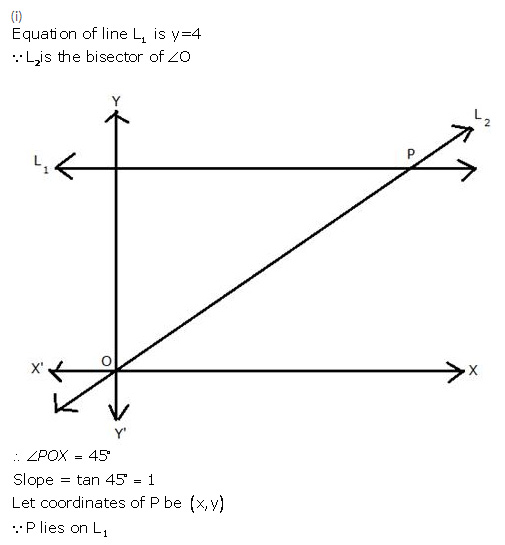
Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 - Equation of a Line

Selina Concise Mathematics Class 10 ICSE Solutions Equation of a Line

Selina Publishers Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line

Equation of a Line Exercise 14A – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.

Find, which of the following points lie on the line x – 2y + 5 = 0:

(i) (1, 3) (ii) (0, 5)

(iii) (-5, 0) (iv) (5, 5)

(v) (2, -1.5) (vi) (-2, -1.5)

Solution:

  

Question 2.

  

Solution:

  
Question 3.

 Solution:

  

Question 4.

For what value of k will the point (3, -k) lie on the line 9x + 4y = 3?

Solution:

The given equation of the line is 9x + 4y = 3.

Put x = 3 and y = -k, we have:

9(3) + 4(-k) = 3

27 – 4k = 3

4k = 27 – 3 = 24

k = 6

Question 5.

Solution:

  

Question 6.

Does the line 3x – 5y = 6 bisect the join of (5, -2) and (-1, 2)?

Solution:

  

Question 7.

(i) The line y = 3x – 2 bisects the join of (a, 3) and (2, -5), find the value of a.

(ii) The line x – 6y + 11 = 0 bisects the join of (8, -1) and (0, k). Find the value of k.

Solution:

  

Question 8.

(i) The point (-3, 2) lies on the line ax + 3y + 6 = 0, calculate the value of a.

(ii) The line y = mx + 8 contains the point (-4, 4), calculate the value of m.

Solution:

(i) Given, the point (-3, 2) lies on the line ax + 3y + 6 = 0.

Substituting x = -3 and y = 2 in the given equation, we have:

a(-3) + 3(2) + 6 = 0

-3a + 12 = 0

3a = 12

a = 4

(ii) Given, the line y = mx + 8 contains the point (-4, 4).

Substituting x = -4 and y = 4 in the given equation, we have:

4 = -4m + 8

4m = 4

m = 1

Question 9.

The point P divides the join of (2, 1) and (-3, 6) in the ratio 2: 3. Does P lie on the line x – 5y + 15 = 0?

Solution:

  

Question 10.

The line segment joining the points (5, -4) and (2, 2) is divided by the point Q in the ratio 1: 2. Does the line x – 2y = 0 contain Q?

Solution:

  

Question 11.

Find the point of intersection of the lines:

4x + 3y = 1 and 3x – y + 9 = 0. If this point lies on the line (2k – 1)x – 2y = 4; find the value of k.

Solution:

Consider the given equations:

4x + 3y = 1 ….(1)

3x – y + 9 = 0 ….(2)

Multiplying (2) with 3, we have:

9x – 3y = -27 ….(3)

Adding (1) and (3), we get,

13x = -26

x = -2

From (2), y = 3x + 9 = -6 + 9 = 3

Thus, the point of intersection of the given lines (1) and (2) is (-2, 3).

The point (-2, 3) lies on the line (2k – 1)x – 2y = 4.

(2k – 1)(-2) – 2(3) = 4

-4k + 2 – 6 = 4

-4k = 8

k = -2

Question 12.

Show that the lines 2x + 5y = 1, x – 3y = 6 and x + 5y + 2 = 0 are concurrent.

Solution:

We know that two or more lines are said to be concurrent if they intersect at a single point.

We first find the point of intersection of the first two lines.

2x + 5y = 1 ….(1)

x – 3y = 6 ….(2)

Multiplying (2) by 2, we get,

2x – 6y = 12 ….(3)

Subtracting (3) from (1), we get,

11y = -11

y = -1

From (2), x = 6 + 3y = 6 – 3 = 3

So, the point of intersection of the first two lines is (3, -1).

If this point lie on the third line, i.e., x + 5y + 2 = 0, then the given lines will be concurrent.

Substituting x = 3 and y = -1, we have:

L.H.S. = x + 5y + 2 = 3 + 5(-1) + 2 = 5 – 5 = 0 = R.H.S.

Thus, (3, -1) also lie on the third line.

Hence, the given lines are concurrent.

Equation of a Line Exercise 14B – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.

  

Solution:

  

Question 2.

  

Solution:

  

Question 3.

Find the slope of the line passing through the following pairs of points:

(i) (-2, -3) and (1, 2)

(ii) (-4, 0) and origin

(iii) (a, -b) and (b, -a)

Solution:

  

Question 4.

Find the slope of the line parallel to AB if:

(i) A = (-2, 4) and B = (0, 6)

(ii) A = (0, -3) and B = (-2, 5)

Solution:

  

Question 5.

Find the slope of the line perpendicular to AB if:

(i) A = (0, -5) and B = (-2, 4)

(ii) A = (3, -2) and B = (-1, 2)

Solution:

  

Question 6.

The line passing through (0, 2) and (-3, -1) is parallel to the line passing through (-1, 5) and (4, a). Find a.

Solution:

  

Question 7.

The line passing through (-4, -2) and (2, -3) is perpendicular to the line passing through (a, 5) and (2, -1). Find a.

Solution:

  

Question 8.

Without using the distance formula, show that the points A (4, -2), B (-4, 4) and C (10, 6) are the vertices of a right-angled triangle.

Solution:

  

Question 9.

Without using the distance formula, show that the points A (4, 5), B (1, 2), C (4, 3) and D (7, 6) are the vertices of a parallelogram.

Solution:

  

Question 10.

(-2, 4), (4, 8), (10, 7) and (11, -5) are the vertices of a quadrilateral. Show that the quadrilateral, obtained on joining the mid-points of its sides, is a parallelogram.

Solution:

  

Question 11.

Show that the points P (a, b + c), Q (b, c + a) and R (c, a + b) are collinear.

Solution:

  

Question 12.

Solution:

  

Question 13.

  

Solution:

  

Question 14.

  

Solution:

  

Question 15.

A (5, 4), B (-3, -2) and C (1, -8) are the vertices of a triangle ABC. Find:

(i) the slope of the altitude of AB,

(ii) the slope of the median AD, and

(iii) the slope of the line parallel to AC.

Solution:

  

Question 16.

  

Solution:

  

Question 17.

  

Solution:

  

Question 18.

The points (-3, 2), (2, -1) and (a, 4) are collinear. Find a.

Solution:

  

Question 19.

The points (K, 3), (2, -4) and (-K + 1, -2) are collinear. Find K.

Solution:

  

Question 20.

Plot the points A (1, 1), B (4, 7) and C (4, 10) on a graph paper. Connect A and B, and also A and C.

Which segment appears to have the steeper slope, AB or AC?

Justify your conclusion by calculating the slopes of AB and AC.

Solution:

  

Question 21.

  

Solution:

  

Equation of a Line Exercise 14C – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.

Find the equation of a line whose:

y-intercept = 2 and slope = 3.

Solution:

Given, y-intercept = c = 2 and slope = m = 3.

Substituting the values of c and m in the equation y = mx + c, we get,

y = 3x + 2, which is the required equation.

Question 2.

Solution:

  

Question 3.

Solution:

  

Question 4.

Solution:

  

Question 5.

Find the equation of the line passing through:

(i) (0, 1) and (1, 2) (ii) (-1, -4) and (3, 0)

Solution:

  

Question 6.

The co-ordinates of two points P and Q are (2, 6) and (-3, 5) respectively. Find:

(i) the gradient of PQ;

(ii) the equation of PQ;

(iii) the co-ordinates of the point where PQ intersects the x-axis.

Solution:

  

Question 7.

The co-ordinates of two points A and B are (-3, 4) and (2, -1). Find:

(i) the equation of AB;

(ii) the co-ordinates of the point where the line AB intersects the y-axis.

Solution:

  

Question 8.

  

Solution:

  

Question 9.

In ΔABC, A = (3, 5), B = (7, 8) and C = (1, -10). Find the equation of the median through A.

Solution:

  

Question 10.

  

Solution:

  

Question 11.

Find the equation of the straight line passing through origin and the point of intersection of the lines x + 2y = 7 and x – y = 4.

Solution:

  

Question 12.

In triangle ABC, the co-ordinates of vertices A, B and C are (4, 7), (-2, 3) and (0, 1) respectively. Find the equation of median through vertex A.

Also, find the equation of the line through vertex B and parallel to AC.

Solution:

  

Question 13.

A, B and C have co-ordinates (0, 3), (4, 4) and (8, 0) respectively. Find the equation of the line through A and perpendicular to BC.

Solution:

  

Question 14.

Find the equation of the perpendicular dropped from the point (-1, 2) onto the line joining the points (1, 4) and (2, 3).

Solution:

  

Question 15.

Find the equation of the line, whose:

(i) x-intercept = 5 and y-intercept = 3

(ii) x-intercept = -4 and y-intercept = 6

(iii) x-intercept = -8 and y-intercept = -4

Solution:

  

Question 16.

Solution:

  

Question 17.

Find the equation of the line with x-intercept 5 and a point on it (-3, 2).

Solution:

  

Question 18.

Find the equation of the line through (1, 3) and making an intercept of 5 on the y-axis.

Solution:

  

Question 19.

Find the equations of the lines passing through point (-2, 0) and equally inclined to the co-ordinate axis.

Solution:

  

Question 20.

  

Solution:

  

Question 21.

  

Solution:

  

Question 22.

A (1, 4), B (3, 2) and C (7, 5) are vertices of a triangle ABC, Find:

(i) the co-ordinates of the centroid of triangle ABC.

(ii) the equation of a line, through the centroid and parallel to AB.

Solution:

  

Question 23.

A (7, -1), B (4, 1) and C (-3, 4) are the vertices of a triangle ABC. Find the equation of a line through the vertex B and the point P in AC; such that AP: CP = 2: 3.

Solution:

Equation of a Line Exercise 14D – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.

Find the slope and y-intercept of the line:

(i) y = 4

(ii) ax – by = 0

(iii) 3x – 4y = 5

Solution:

  

Question 2.

The equation of a line x – y = 4. Find its slope and y-intercept. Also, find its inclination.

Solution:

  

Question 3.

(i) Is the line 3x + 4y + 7 = 0 perpendicular to the line 28x – 21y + 50 = 0?

(ii) Is the line x – 3y = 4 perpendicular to the line 3x – y = 7?

(iii) Is the line 3x + 2y = 5 parallel to the line x + 2y = 1?

(iv) Determine x so that the slope of the line through (1, 4) and (x, 2) is 2.

Solution:

Question 4.

  

Solution:

  

Question 5.

Solution:

  

Question 6.

(i) Lines 2x – by + 3 = 0 and ax + 3y = 2 are parallel to each other. Find the relation connecting a and b.

(ii) Lines mx + 3y + 7 = 0 and 5x – ny – 3 = 0 are perpendicular to each other. Find the relation connecting m and n.

Solution:

  

Question 7.

Find the value of p if the lines, whose equations are 2x – y + 5 = 0 and px + 3y = 4 are perpendicular to each other.

Solution:

  

Question 8.

The equation of a line AB is 2x – 2y + 3 = 0.

(i) Find the slope of the line AB.

(ii) Calculate the angle that the line AB makes with the positive direction of the x-axis.

Solution:

  

Question 9.

The lines represented by 4x + 3y = 9 and px – 6y + 3 = 0 are parallel. Find the value of p.

Solution:

  

Question 10.

If the lines y = 3x + 7 and 2y + px = 3 are perpendicular to each other, find the value of p.

Solution:

  

Question 11.

The line through A(-2,3) and B(4,b) is perpendicular to the line 2x – 4y =5. Find the value of b.

Solution:

  

Question 12.

Find the equation of the line through (-5, 7) and parallel to:

(i) x-axis (ii) y-axis

Solution:

  

Question 13.

(i) Find the equation of the line passing through (5, -3) and parallel to x – 3y = 4.

(ii) Find the equation of the line parallel to the line 3x + 2y = 8 and passing through the point (0, 1).

Solution:

  

Question 14.

Find the equation of the line passing through (-2, 1) and perpendicular to 4x + 5y = 6.

Solution:

  

Question 15.

Find the equation of the perpendicular bisector of the line segment obtained on joining the points (6, -3) and (0, 3).

Solution:

  

Question 16.

  

Solution:

  

Question 17.

B (-5, 6) and D (1, 4) are the vertices of rhombus ABCD. Find the equation of diagonal BD and of diagonal AC.

Solution:

  

Question 18.

A = (7, -2) and C = (-1, -6) are the vertices of square ABCD. Find the equations of diagonal BD and of diagonal AC.

Solution:

  

Question 19.

A (1, -5), B (2, 2) and C (-2, 4) are the vertices of triangle ABC, find the equation of:

(i) the median of the triangle through A.

(ii) the altitude of the triangle through B.

(iii) the line through C and parallel to AB.

Solution:

  

Question 20.

(i) Write down the equation of the line AB, through (3, 2) and perpendicular to the line 2y = 3x + 5.

(ii) AB meets the x-axis at A and the y-axis at B. Write down the co-ordinates of A and B. Calculate the area of triangle OAB, where O is the origin.

Solution:

  

Question 21.

The line 4x – 3y + 12 = 0 meets the x-axis at A. Write the co-ordinates of A.

Determine the equation of the line through A and perpendicular to 4x – 3y + 12 = 0.

Solution:

  

Question 22.

The point P is the foot of perpendicular from A (-5, 7) to the line whose equation is 2x – 3y + 18 = 0. Determine:

(i) the equation of the line AP

(ii) the co-ordinates of P

Solution:

  

Question 23.

The points A, B and C are (4, 0), (2, 2) and (0, 6) respectively. Find the equations of AB and BC.

If AB cuts the y-axis at P and BC cuts the x-axis at Q, find the co-ordinates of P and Q.

Solution:

  

Question 24.

  

Solution:

  

Question 25.

Find the value of a for which the points A(a, 3), B(2, 1) and C(5, a) are collinear. Hence, find the equation of the line.

Solution:

Equation of a Line Exercise 14E – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.

Point P divides the line segment joining the points A (8, 0) and B (16, -8) in the ratio 3: 5. Find its co-ordinates of point P.

Also, find the equation of the line through P and parallel to 3x + 5y = 7.

Solution:

  

Question 2.

The line segment joining the points A(3, -4) and B (-2, 1) is divided in the ratio 1: 3 at point P in it. Find the co-ordinates of P. Also, find the equation of the line through P and perpendicular to the line 5x – 3y + 4 = 0.

Solution:

Question 3.

A line 5x + 3y + 15 = 0 meets y-axis at point P. Find the co-ordinates of point P. Find the equation of a line through P and perpendicular to x – 3y + 4 = 0.

Solution:

Question 4.

Find the value of k for which the lines kx – 5y + 4 = 0 and 5x – 2y + 5 = 0 are perpendicular to each other.

Solution:

Question 5.

Solution:

Question 6.

(1, 5) and (-3, -1) are the co-ordinates of vertices A and C respectively of rhombus ABCD. Find the equations of the diagonals AC and BD.

Solution:

Question 7.

Show that A (3, 2), B (6, -2) and C (2, -5) can be the vertices of a square.

(i) Find the co-ordinates of its fourth vertex D, if ABCD is a square.

(ii) Without using the co-ordinates of vertex D, find the equation of side AD of the square and also the equation of diagonal BD.

Solution:

 

Question 8.

A line through origin meets the line x = 3y + 2 at right angles at point X. Find the co-ordinates of X.

Solution:

Question 9.

A straight line passes through the point (3, 2) and the portion of this line, intercepted between the positive axes, is bisected at this point. Find the equation of the line.

Solution:

Question 10.

Find the equation of the line passing through the point of intersection of 7x + 6y = 71 and 5x – 8y = -23; and perpendicular to the line 4x – 2y = 1.

Solution:

  

Question 11.

Solution:

  

Question 12.

O (0, 0), A (3, 5) and B (-5, -3) are the vertices of triangle OAB. Find:

(i) the equation of median of triangle OAB through vertex O.

(ii) the equation of altitude of triangle OAB through vertex B.

Solution:

  

Question 13.

Determine whether the line through points (-2, 3) and (4, 1) is perpendicular to the line 3x = y + 1.

Does the line 3x = y + 1 bisect the line segment joining the two given points?

Solution:

  

Question 14.

Solution:

  

Question 15.

Find the value of k such that the line (k – 2)x + (k + 3)y – 5 = 0 is:

(i) perpendicular to the line 2x – y + 7 = 0

(ii) parallel to it.

Solution:

  

Question 16.

The vertices of a triangle ABC are A (0, 5), B (-1, -2) and C (11, 7). Write down the equation of BC. Find:

(i) the equation of line through A and perpendicular to BC.

(ii) the co-ordinates of the point, where the perpendicular through A, as obtained in (i), meets BC.

Solution:

  

Question 17.

  

Solution:

  

Question 18.

P (3, 4), Q (7, -2) and R (-2, -1) are the vertices of triangle PQR. Write down the equation of the median of the triangle through R.

Solution:

  

Question 19.

A (8, -6), B (-4, 2) and C (0, -10) are vertices of a triangle ABC. If P is the mid-point of AB and Q is the mid-point of AC, use co-ordinate geometry to show that PQ is parallel to BC. Give a special name of quadrilateral PBCQ.

Solution:

  

Question 20.

A line AB meets the x-axis at point A and y-axis at point B. The point P (-4, -2) divides the line segment AB internally such that AP : PB = 1 : 2. Find:

(i) the co-ordinates of A and B.

(ii) the equation of line through P and perpendicular to AB.

Solution:

  

Question 21.

A line intersects x-axis at point (-2, 0) and cuts off an intercept of 3 units from the positive side of y-axis. Find the equation of the line.

Solution:

  

Question 22.

Find the equation of a line passing through the point (2, 3) and having the x-intercept of 4 units.

Solution:

  

Question 23.

  

Solution:

  

Question 24.

  

Solution:

  

Question 25.

The ordinate of a point lying on the line joining the points (6, 4) and (7, -5) is -23. Find the co-ordinates of that point.

Solution:

  

Question 26.

Points A and B have coordinates (7, -3) and (1, 9) respectively. Find:

(i) the slope of AB.

(ii) the equation of the perpendicular bisector of the line segment AB.

(iii) the value of ‘p’ if (-2, p) lies on it.

Solution:

  

Question 27.

  

Solution:

  

Question 28.

The equation of a line 3x + 4y – 7 = 0. Find:

(i) the slope of the line.

(ii) the equation of a line perpendicular to the given line and passing through the intersection of the lines x – y + 2 = 0 and 3x + y – 10 = 0.

Solution:

  

Question 29.

ABCD is a parallelogram where A(x, y), B(5, 8), C(4, 7) and D(2, -4). Find:

(i) Co-ordinates of A

(ii) Equation of diagonal BD

Solution:

  

Question 30.

  

Solution:

Question 31.

  

Solution:

  

Question 32.

Find the equation of the line that has x-intercept = -3 and is perpendicular to 3x + 5y = 1.

Solution:

  

Question 33.

A straight line passes through the points P(-1, 4) and Q(5, -2). It intersects x-axis at point A and y-axis at point B. M is the mid- t point of the line segment AB. Find:

(i) the equation of the line.

(ii) the co-ordinates of points A and B.

(iii) the co-ordinates of point M

Solution:

  

Question 34.

  

Solution:

  

Question 35.

A line through point P(4, 3) meets x-axis at point A and the y-axis at point B. If BP is double of PA, find the equation of AB.

Solution:

  

Question 36.

Find the equation of line through the intersection of lines 2x – y = 1 and 3x + 2y = -9 and making an angle of 30° with positive direction of x-axis.

Solution:

  

Question 37.

Find the equation of the line through the Points A(-1, 3) and B(0, 2). Hence, show that the points A, B and C(1, 1) are collinear.

Solution:

  

Question 38.

Three vertices of a parallelogram ABCD taken in order are A(3, 6), B(5, 10) and C(3, 2), find :

(i) the co-ordinates of the fourth vertex D.

(ii) length of diagonal BD.

(iii) equation of side AB of the parallelogram ABCD.

Solution:

  

Question 39.

  

Solution:

  

Question 40.

  

Question 41.

i. Since A lies on the X-axis, let the co-ordinates of A be (x, 0).

Since B lies on the Y-axis, let the co-ordinates of B be (0, y).

Let m = 1 and n = 2

Using Section formula,

  

⇒ Slope of line perpendicular to AB = m = -2

P = (4, -1)

Thus, the required equation is

y – y1 = m(x – x1)

⇒ y – (-1) = -2(x – 4)

⇒ y + 1 = -2x + 8

⇒ 2x + y = 7

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 - Equation of a Line