Selina Concise Mathematics Class 9 ICSE Maths Solutions Chapter 16 - Area Theorems [Proof and Use]

Selina Concise Mathematics Class 9 ICSE Solutions Area Theorems [Proof and Use]

Selina ICSE Solutions for Class 9 Maths Chapter 16 Area Theorems [Proof and Use]

Exercise 16(A)

1.In the given figure, if area of triangle ADE is 60 cm2, state, given reason, the area of :

(i) Parallelogram ABED;

(ii) Rectangle ABCF;

(iii) Triangle ABE.



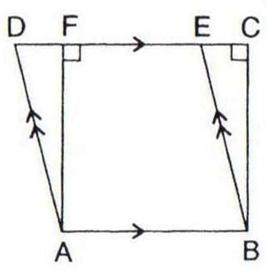
Solution 1:

2.The given figure shows a rectangle ABDC and a parallelogram ABEF; drawn on opposite sides of AB. Prove that:

(i) Quadrilateral CDEF is a parallelogram;

(ii) Area of quad. CDEF

= Area of rect. ABDC

+ Area of // gm. ABEF.



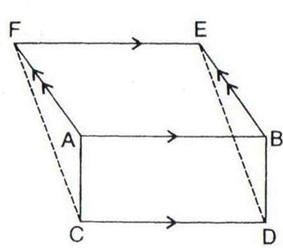
Solution 2:

Since from the figure, we get CD//FE therefore FC must parallel to DE. Therefore it is proved that the quadrilateral CDEF is a parallelogram.
Area of parallelogram on same base and between same parallel lines is always equal and area of parallelogram is equal to the area of rectangle on the same base and of the same altitude i.e, between same parallel lines.
So Area of CDEF= Area of ABDC + Area of ABEF
Hence Proved

3.In the given figure, diagonals PR and QS of the parallelogram PQRS intersect at point O and LM is parallel to PS. Show that:

(i) 2 Area (POS) = Area (// gm PMLS)

(ii) Area (POS) + Area (QOR)

= Area (// gm PQRS)

(iii) Area (POS) + Area (QOR)

= Area (POQ) + Area (SOR).

Solution 3:

4.In parallelogram ABCD, P is a point on side AB and Q is a point on side BC.

Prove that:

(i) CPD and AQD are equal in area.

(ii) Area (AQD)

= Area (APD) + Area (CPB)

Solution 4:

Given ABCD is a parallelogram. P and Q are any points on the sides AB and BC respectively, join diagonals AC and BD.
proof:
since triangles with same base and between same set of parallel lines have equal areas
area (CPD)=area(BCD)…… (1)
again, diagonals of the parallelogram bisects area in two equal parts
area (BCD)=(1/2) area of parallelogram ABCD…… (2)
from (1) and (2)
area(CPD)=1/2 area(ABCD)…… (3)
similarly area (AQD)=area(ABD)=1/2 area(ABCD)…… (4)
from (3) and (4)
area(CPD)=area(AQD),
hence proved.
(ii)
We know that area of triangles on the same base and between same parallel lines are equal
So Area of AQD= Area of ACD= Area of PDC = Area of BDC = Area of ABC=Area of APD + Area of BPC
Hence Proved

5.In the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD.




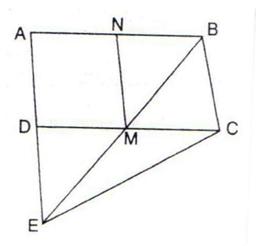
If the area of parallelogram ABCD is 48 cm2;

(i) State the area of the triangle BEC.

(ii) Name the parallelogram which is equal in area to the triangle BEC.

Solution 5:

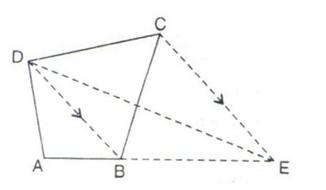
6.In the following figure, CE is drawn parallel to diagonals DB of the quadrilateral ABCD which meets AB produced at point E.

Prove that ADE and quadrilateral ABCD are equal in area.

Solution 6:

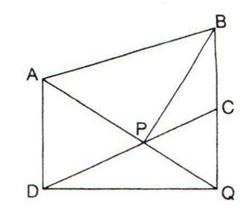
7.ABCD is a parallelogram a line through A cuts DC at point P and BC produced at Q. Prove that triangle BCP is equal in area to triangle DPQ.



Solution 7:

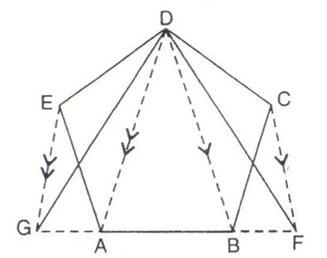
8.The given figure shows a pentagon ABCDE. EG drawn parallel to DA meets BA produced at G and CF draw parallel to DB meets AB produced at F.

Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.



Solution 8:

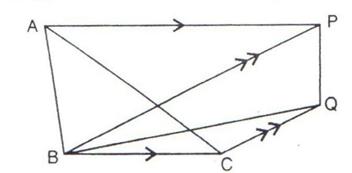
9.In the given figure, AP is parallel to BC, BP is parallel to CQ. Prove that the area of triangles ABC and BQP are equal.



Solution 9:

10.In the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.

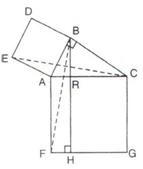
If BH is perpendicular to FG prove that:

(i) EAC BAF.

(ii) Area of the square ABDE

= Area of the rectangle ARHF.

Solution 10:

11.In the following figure, DE is parallel to BC. Show that:

(i) Area (ADC) = Area(AEB).

(ii) Area (BOD) = Area (COE).

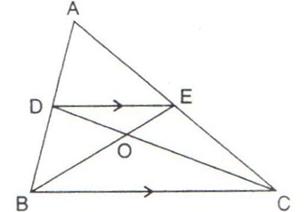
Solution 11:

12.ABCD and BCFE are parallelograms. If area of triangle EBC = 480 cm2; AB = 30 cm and BC = 40 cm; Calculate;

(i) Area of parallelogram ABCD;

(ii) Area of the parallelogram BCFE;

(iii) Length of altitude from A on CD;

(iv) Area of triangle ECF.




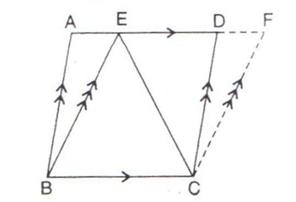
Solution 12:

13.In the given figure, D is mid-point of side AB of ABC and BDEC is a parallelogram.

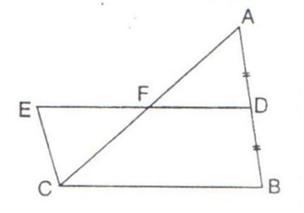
Prove that:

Area of ABC = Area of // gm BDEC.

Solution 13:

14.In the following, AC // PS // QR and PQ // DB // SR.

Prove that:

Area of quadrilateral PQRS = 2 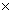Area of quad. ABCD.

Solution 14:

15.ABCD is trapezium with AB // DC. A line parallel to AC intersects AB at point M and BC at point N. Prove that: area of Δ ADM = area of Δ ACN.

Solution 15:

16.In the given figure, AD // BE // CF. Prove that area (ΔAEC) = area (ΔDBF)

 

Solution 16:

We know that area of triangles on the same base and between same parallel lines are equal.
Consider ABED quadrilateral; AD||BE
With common base, BE and between AD and BE parallel lines, we have
Area of ΔABE = Area of ΔBDE
Similarly, in BEFC quadrilateral, BE||CF
With common base BC and between BE and CF parallel lines, we have
Area of ΔBEC = Area of ΔBEF
Adding both equations, we have
Area of ΔABE + Area of ΔBEC = Area of ΔBEF + Area of ΔBDE
=> Area of AEC = Area of DBF
Hence Proved

17.In the given figure, ABCD is a parallelogram; BC is produced to point X. Prove that: area (Δ ABX) = area (quad. ACXD)

 

Solution 17:

Given: ABCD is a parallelogram.
We know that
Area of ΔABC = Area of ΔACD
Consider ΔABX,
Area of ΔABX = Area of ΔABC + Area of ΔACX
We also know that area of triangles on the same base and between same parallel lines are equal.
Area of ΔACX = Area of ΔCXD
From above equations, we can conclude that
Area of ΔABX = Area of ΔABC + Area of ΔACX = Area of ΔACD+ Area of ΔCXD = Area of ACXD Quadrilateral
Hence Proved

18.The given figure shows parallelograms ABCD and APQR. Show that these parallelograms are equal in area.

[Join B and R]

 

Solution 18:

Join B and R and P and R.
We know that the area of the parallelogram is equal to twice the area of the triangle, if the triangle and the parallelogram are on the same base and between the parallels
Consider ABCD parallelogram:
Since the parallelogram ABCD and the triangle ABR lie on AB and between the parallels AB and DC, we have

Exercise 16(B)

1.Show that:

(i) A diagonal divides a parallelogram into two triangles of equal area.

(ii) The ratio of the areas of two triangles of the same height is equal to the ratio of their bases.

(iii) The ratio of the areas of two triangles on the same base is equal to the ratio of their heights.

Solution 1:

2.In the given figure; AD is median of ABC and E is any point on median AD. Prove that Area (ABE) = Area (ACE).

Solution 2:

3.In the figure of question 2, if E is the mid point of median AD, then prove that:

Area (ABE) = 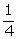Area (ABC).

Solution 3:

4.ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD respectively.

Prove that area of triangle APQ = 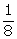of the area of parallelogram ABCD.

Solution 4:

We have to join PD and BD.

5.The base BC of triangle ABC is divided at D so that BD = DC.

Prove that area of ABD = 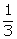of the area of ABC.

Solution 5:

6.In a parallelogram ABCD, point P lies in DC such that DP: PC = 3:2. If area of ΔDPB = 30 sq. cm, find the area of the parallelogram ABCD.

Solution 6:

Ratio of area of triangles with same vertex and bases along the same line is equal to ratio of their respective bases. So, we have

7.ABCD is a parallelogram in which BC is produced to E such that CE = BC and AE intersects CD at F.

 

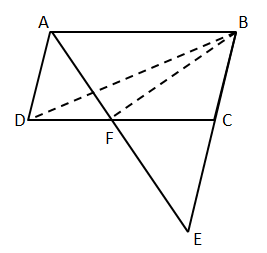
If ar.(∆DFB) = 30 cm²; find the area of parallelogram

Solution 7:

8.The following figure shows a triangle ABC in which P, Q and R are mid-points of sides AB, BC and CA respectively. S is mid-point of PQ:

Prove that: ar.(∆ ABC) = 8 × ar.(∆ QSB)

 

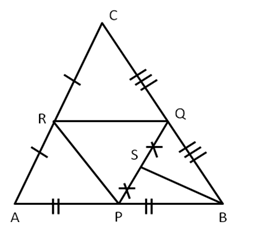
Solution 8:

Exercise 16(C)

1.In the given figure, the diagonals AC and BD intersect at point O. If OB = OD and AB//DC, show that:

(i) Area (Δ DOC) = Area (Δ AOB).

(ii) Area (Δ DCB) = Area (Δ ACB).

(iii) ABCD is a parallelogram.

  

Solution 1:

2.The given figure shows a parallelogram ABCD with area 324 sq. cm. P is a point in AB such that AP:PB = 1:2 Find The area of Δ APD.

  

Solution 2:

3.In ABC, E and F are mid-points of sides AB and AC respectively. If BF and CE intersect each other at point O, prove that the OBC and quadrilateral AEOF are equal in area.

Solution 3:

4.In parallelogram ABCD, P is mid-point of AB. CP and BD intersect each other at point O. If area of POB = 40 cm², and OP : OC = 1:2, find:

(i) Areas of BOC and PBC

(ii) Areas of ABC and parallelogram ABCD.

Solution 4:

5.The medians of a triangle ABC intersect each other at point G. If one of its medians is AD, prove that:

(i) Area (ABD) = 3 Area (BGD)

(ii) Area (ACD) = 3 Area (CGD)

(iii) Area (BGC) = Area (ABC)

Solution 5:

6.The perimeter of a triangle ABC is 37 cm and the ratio between the lengths of its altitudes be 6 : 5 : 4. Find the lengths of its sides.

Let the sides be x cm, y cm and (37 - x - y) cm. Also, let the lengths of altitudes be 6a cm, 5a cm and 4a cm.

Solution 6:

7.

Solution 7:

8.

Solution 8:

9.In the following figure, OAB is a triangle and AB∥DC.

 

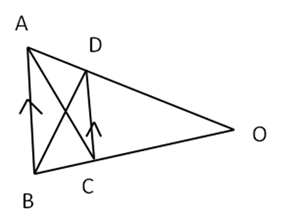
If the area of ∆ CAD = 140 cm² and the area of ∆ ODC = 172 cm², find

(i) the area of ∆ DBC

(ii) the area of ∆ OAC

(iii) the area of ∆ ODB.

Solution 9:

Selina Concise Mathematics Class 9 ICSE Maths Solutions Chapter 16 - Area Theorems [Proof and Use]