Selina Concise Mathematics Class 9 ICSE Math Solutions Chapter 22 - Trigonometrical Ratios

Selina Concise Mathematics Class 9 ICSE Solutions Trigonometrical Ratios

Selina ICSE Solutions for Class 9 Maths Chapter 22 Trigonometrical Ratios [Sine, Consine, Tangent of an Angle and their Reciprocals]

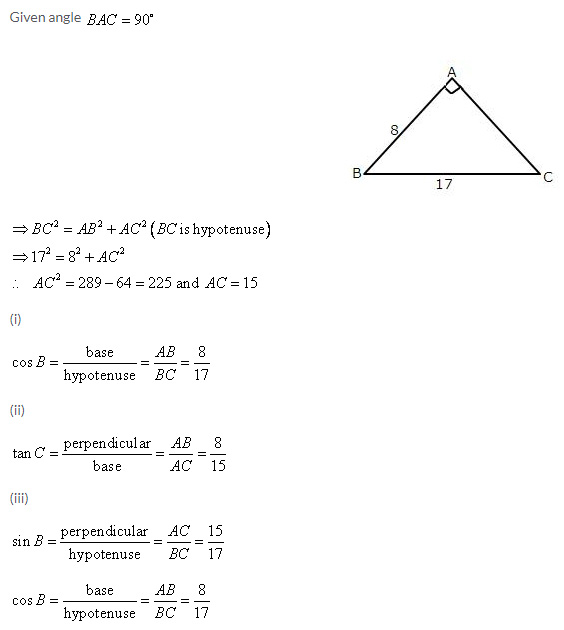
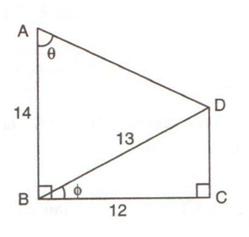
Exercise 22(A)

1. From the following figure, find the values of :

(i) sin A

(ii) cos A

(iii) cot A

(iv) sec C

(v) cosec C

(vi) tan C.

Solution 1:

2.Form the following figure, find the values of :

(i) cos B

(ii) tan C

(iii) sin²B + cos²B

(iv) sin B. cos C + cos B. sin C

Solution 2:

3.From the following figure, find the values of :

(i) cos A (ii) cosec A

(iii) tan²A - sec²A (iv) sin C

(v) sec C (vi) cot² C -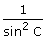 

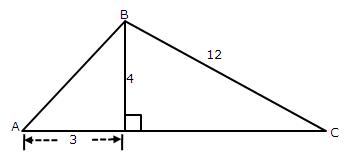
Solution 3:

4.From the following figure, find the values of :

(i) sin B (ii) tan C

(iii) sec² B - tan²B (iv) sin²C + cos²C

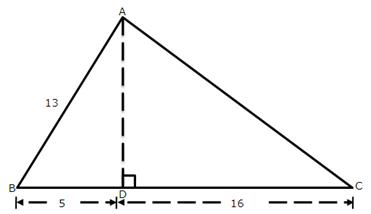
Solution 4:

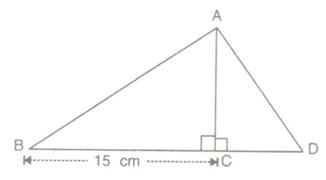
5.Given: sin A = 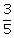, find :

(i) tan A(ii) cos A

Solution 5:

6.From the following figure, find the values of :

(i) sin A

(ii) sec A

(iii) cos² A + sin²A

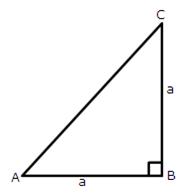
Solution 6:

7.Given: cos A =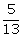 

Evaluate: (i) 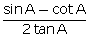(ii) 

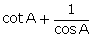
Solution 7:

8.Given: sec A = 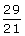, evaluate : sin A -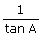 

Solution 8:

9.Given: tan A = 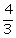, find :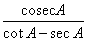 

Solution 9:

10.Given: 4 cot A = 3 find;

(i) sin A

(ii) sec A

(iii) cosec² A - cot²A.

Solution 10:

11.Given: cos A = 0.6; find all other trigonometrical ratios for angle A.

Solution 11:

12.In a right-angled triangle, it is given that A is an acute angle and tan A =.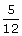

find the value of :

(i) cos A(ii) sin A(iii)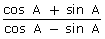 

Solution 12:

13.Given: sin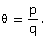 

Find cos 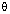+ sin 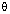in terms of p and q.

Solution 13:

14.If cos A = 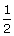and sin B = 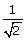, find the value of : . 

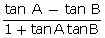Are angles A and B from the same triangle? Explain.

Solution 14:

15.If 5 cot 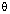= 12, find the value of : Cosec 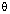+ sec 

Solution 15:

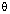
16.If tan x = 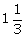, find the value of : 4 sin²x - 3 cos²x + 2

Solution 16:

17.Ifcosec 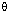= 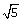, find the value of:

(i) 2 - sin² 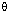- cos²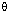 

(ii)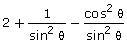 

Solution 17:

18.If sec A = 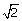, find the value of :

Solution 18:

19.If sec A = 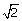, find the value of :

Solution 19:

20.In the following figure:

AD 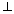BC, AC = 26 CD = 10, BC = 42,

DAC = x and B = y.

Find the value of :

(i) cot x

(ii)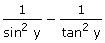 

(iii)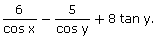 

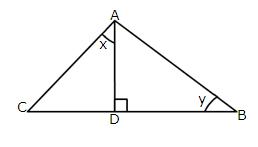
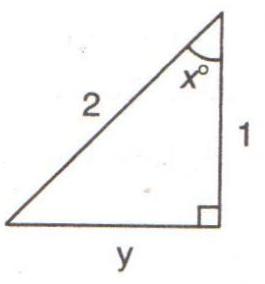
 Solution 20:

Exercise 22(B)

1.From the following figure, find:

(i) y (ii) sin x^o

(iii) (sec x^o - tan x^o) (sec x^o + tan x^o)

Solution 1:

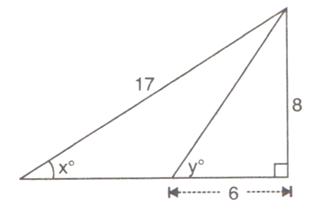
2.Use the given figure to find:

(i) sin x^o (ii) cos y^o

(iii) 3 tan x^o - 2 sin y^o + 4 cos y^o.

Solution 2:

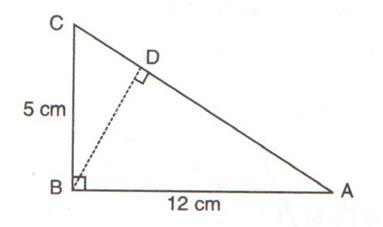
3.In the diagram, given below, triangle ABC is right-angled at B and BD is perpendicular to AC. Find:

(i) cos DBC (ii) cot DBA

Solution 3:

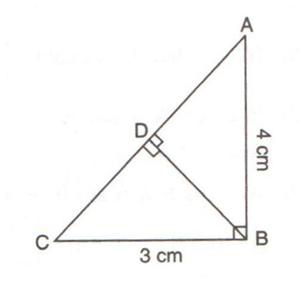
4.In the given figure, triangle ABC is right-angled at B. D is the foot of the perpendicular from B to AC. Given that BC = 3 cm and AB = 4 cm. find:

(i) tan 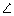DBC

(ii) sin 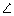DBA

Solution 4:

5.In triangle ABC, AB = AC = 15 cm and BC = 18 cm, find cos ABC.

Solution 5:

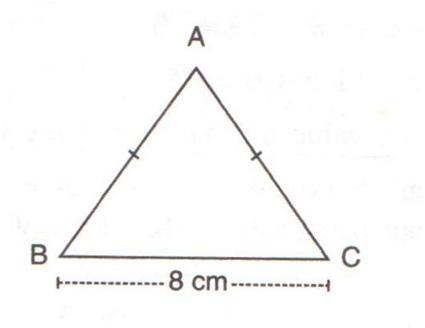
6.In the figure given below, ABC is an isosceles triangle with BC = 8 cm and AB = AC = 5 cm. Find:

(i) sin B (ii) tan C

(iii) sin² B + cos²B (iv) tan C - cot B

Solution 6:

7.In triangle ABC; ABC = 90^o, CAB = x^o, tan x^o = 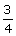and BC = 15 cm. Find the measures of AB and AC.

Solution 7:

8.Using the measurements given in the following figure:

(i) Find the value of sin 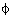and tan.

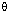(ii) Write an expression for AD in terms of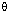 

Solution 8:

9.In the given figure;

BC = 15 cm and sin B =.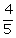

(i) Calculate the measure of AB and AC.

(ii) Now, if tan ADC = 1; calculate the measures of CD and AD.

Also, show that: tan²B -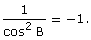 

Solution 9:

10.If sin A + cosec A = 2;

Find the value of sin² A + cosec² A.

Solution 10:

11.If tan A + cot A = 5;

Find the value of tan² A + cot² A.

Solution 11:

12.Given: 4 sin 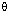= 3 cos 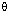; find the value of:

(i) sin 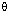(ii) cos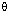 

(iii) cot² 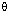- cosec².

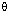(iv) 4 cos²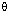- 3 sin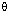²+ 2

Solution 12:

13.Given : 17 cos 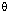= 15;

Find the value of: tan 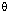+ 2 sec.

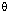Solution 13:

14.Given : 5 cos A - 12 sin A = 0; evaluate  :

.

Solution 14:

15.In the given figure; 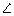C = 90^o and D is mid-point of AC. Find

(i) 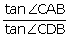 (ii) 

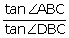
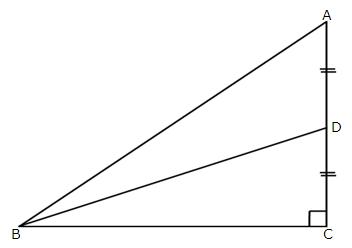
Solution 15:

16.If 3 cos A = 4 sin A, find the value of :

(i) cos A(ii) 3 - cot² A + cosec²A.

Solution 16:

17.In triangle ABC, 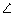B = 90^o and tan A = 0.75. If AC = 30 cm, find the lengths of AB and BC.

Solution 17:

18.In rhombus ABCD, diagonals AC and BD intersect each other at point O.

If cosine of angle CAB is 0.6 and OB = 8 cm, find the lengths of the the side and the diagonals of the rhombus.

Solution 18:

19.In triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find:

(i) cos B (ii) sin C

(iii) tan² B - sec² B + 2

Solution 19:

20.In triangle ABC, AD is perpendicular to BC. sin B = 0.8, BD = 9 cm and tan C = 1. Find the length of AB, AD, AC and DC.

Solution 20:

21.Given q tan A = p, find the value of :

.

Solution 21:

22.If sin A = cos A, find the value of 2 tan²A - 2 sec² A + 5.

Solution 22:

23.In rectangle ABCD, diagonal BD = 26 cm and cotangent of angle ABD = 1.5. Find the area and the perimeter of the rectangle ABCD.

Solution 23:

24.If 2 sin x = 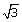, evaluate.

(i) 4 sin³ x - 3 sin x.

(ii) 3 cos x - 4 cos³ x.

Solution 24:

25.If sin A = 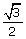 and cos B = 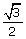, find the value of : .

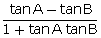Solution 25:

26.Use the informations given in the following figure to evaluate: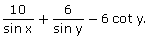 

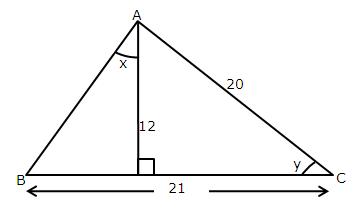
Solution 26:

27.If sec A = 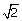, find: .

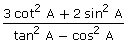Solution 27:

28.If 5 cos 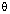 = 3, evaluate : .

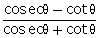Solution 28:

29.If cosec A + sin A = 5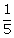, find the value of cosec²A + sin²A.

Solution 29:

30.If 5 cos 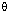 = 6 sin 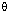; evaluate:

(i) tan 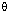 (ii) 

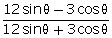
Solution 30:

Selina Concise Mathematics Class 9 ICSE Math Solutions Chapter 22 - Trigonometrical Ratios