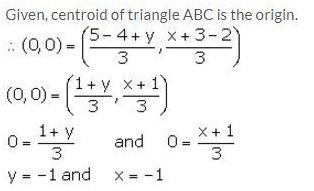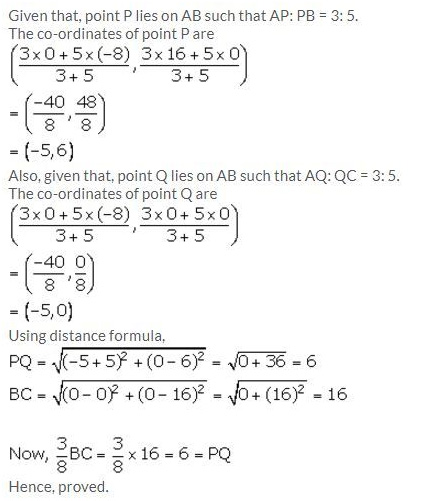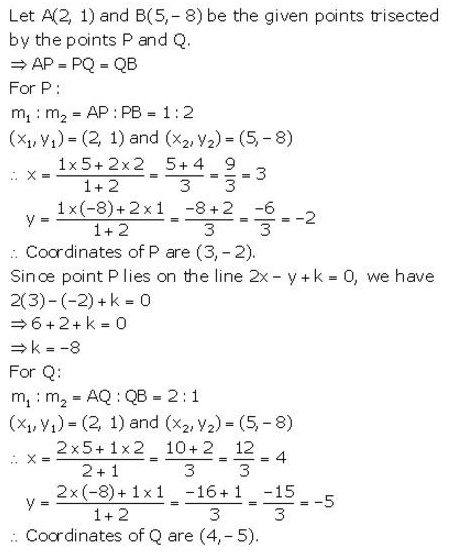Selina Concise Mathematics Class 10 ICSE Solutions Section and Mid-Point Formula
Selina Publishers Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula
Section and Mid-Point Formula Exercise 13A – Selina Concise Mathematics Class 10 ICSE Solutions
Question 1.
Calculate the co-ordinates of the point P which divides the line segment joining:
(i) A (1, 3) and B (5, 9) in the ratio 1: 2.
(ii) A (-4, 6) and B (3, -5) in the ratio 3: 2.
Solution:
Question 2.
In what ratio is the line joining (2, -3) and (5, 6) divided by the x-axis.
Solution:
Let the line joining points A (2, -3) and B (5, 6) be divided by point P (x, 0) in the ratio k: 1.
Question 3.
In what ratio is the line joining (2, -4) and (-3, 6) divided by the y-axis.
Solution:
Let the line joining points A (2, -4) and B (-3, 6) be divided by point P (0, y) in the ratio k: 1.
Question 4.
In what ratio does the point (1, a) divided the join of (-1, 4) and (4, -1)? Also, find the value of a.
Solution:
In what ratio does the point (a, 6) divide the join of (-4, 3) and (2, 8)? Also, find the value of a.
Solution:
Let the point P (a, 6) divides the line segment joining A (-4, 3) and B (2, 8) in the ratio k: 1.
Using section formula, we have:
Question 6.
In what ratio is the join of (4, 3) and (2, -6) divided by the x-axis. Also, find the co-ordinates of the point of intersection.
Solution:
Let the point P (x, 0) on x-axis divides the line segment joining A (4, 3) and B (2, -6) in the ratio k: 1.
Using section formula, we have:
Question 7.
Find the ratio in which the join of (-4, 7) and (3, 0) is divided by the y-axis. Also, find the coordinates of the point of intersection.
Solution:
Let S (0, y) be the point on y-axis which divides the line segment PQ in the ratio k: 1.
Using section formula, we have:
Points A, B, C and D divide the line segment joining the point (5, -10) and the origin in five equal parts. Find the co-ordinates of A, B, C and D.
Solution:
Question 9.
The line joining the points A (-3, -10) and B (-2, 6) is divided by the point P such that Find the co-ordinates of P.
Find the co-ordinates of P.
 Find the co-ordinates of P.
Find the co-ordinates of P.
Solution:
Question 10.
P is a point on the line joining A (4, 3) and B (-2, 6) such that 5AP = 2BP. Find the co-ordinates of P.
Solution:
Calculate the ratio in which the line joining the points (-3, -1) and (5, 7) is divided by the line x = 2. Also, find the co-ordinates of the point of intersection.
Solution:
The co-ordinates of every point on the line x = 2 will be of the type (2, y).
Using section formula, we have:
Question 12.
Calculate the ratio in which the line joining A (6, 5) and B (4, -3) is divided by the line y = 2.
Solution:
The co-ordinates of every point on the line y = 2 will be of the type (x, 2).
Using section formula, we have:
Question 13.
The point P (5, -4) divides the line segment AB, as shown in the figure, in the ratio 2: 5. Find the co-ordinates of points A and B.
Solution:
Question 14.
Find the co-ordinates of the points of trisection of the line joining the points (-3, 0) and (6, 6).
Solution:
Let P and Q be the point of trisection of the line segment joining the points A (-3, 0) and B (6, 6).
So, AP = PQ = QB
Question 15.
Show that the line segment joining the points (-5, 8) and (10, -4) is trisected by the co-ordinate axes.
Solution:
Let P and Q be the point of trisection of the line segment joining the points A (-5, 8) and B (10, -4).
So, AP = PQ = QB
Hence, the line segment joining the given points A and B is trisected by the co-ordinate axes.
Question 16.
Show that A (3, -2) is a point of trisection of the line-segment joining the points (2, 1) and (5, -8). Also, find the co-ordinates of the other point of trisection.
Solution:
Let A and B be the point of trisection of the line segment joining the points P (2, 1) and Q (5, -8).
So, PA = AB = BQ
Question 17.
If A = (-4, 3) and B = (8, -6)
(i) Find the length of AB.
(ii) In what ratio is the line joining A and B, divided by the x-axis?
Solution:
Question 18.
The line segment joining the points M (5, 7) and N (-3, 2) is intersected by the y-axis at point L. Write down the abscissa of L. Hence, find the ratio in which L divides MN. Also, find the co-ordinates of L.
Solution:
Since, point L lies on y-axis, its abscissa is 0.
Let the co-ordinates of point L be (0, y). Let L divides MN in the ratio k: 1.
Question 19.
A (2, 5), B (-1, 2) and C (5, 8) are the co-ordinates of the vertices of the triangle ABC. Points P and Q lie on AB and AC respectively, such that AP: PB = AQ: QC = 1: 2.
(i) Calculate the co-ordinates of P and Q.
(ii) Show that PQ = 1/3 BC.
Solution:
Question 20.
A (-3, 4), B (3, -1) and C (-2, 4) are the vertices of a triangle ABC. Find the length of line segment AP, where point P lies inside BC, such that BP: PC = 2: 3.
Solution:
Question 21.
The line segment joining A (2, 3) and B (6, -5) is intercepted by x-axis at the point K. Write down the ordinate of the point K. Hence, find the ratio in which K divides AB. Also, find the co-ordinates of the point K.
Solution:
Question 22.
The line segment joining A (4, 7) and B (-6, -2) is intercepted by the y-axis at the point K. Write down the abscissa of the point K. Hence, find the ratio in which K divides AB. Also, find the co-ordinates of the point K.
Solution:
Question 23.
The line joining P (-4, 5) and Q (3, 2) intersects the y-axis at point R. PM and QN are perpendiculars from P and Q on the x-axis. Find:
(i) the ratio PR: RQ.
(ii) the co-ordinates of R.
(iii) the area of the quadrilateral PMNQ.
Solution:
In the given figure, line APB meets the x-axis at point A and y-axis at point B. P is the point (-4, 2) and AP: PB = 1: 2. Find the co-ordinates of A and B.
Solution:
Given, A lies on x-axis and B lies on y-axis.
Let the co-ordinates of A and B be (x, 0) and (0, y) respectively.
Given, P is the point (-4, 2) and AP: PB = 1: 2.
Using section formula, we have:
Thus, the co-ordinates of points A and B are (-6, 0) and (0, 6) respectively.
Question 25.
Given a line segment AB joining the points A(-4, 6) and B(8, -3). Find:
(i) the ratio in which AB is divided by the y-axis
(ii) find the coordinates of the point of intersection
(iii) the length of AB
Solution:
Question 26.
If P(-b, 9a – 2) divides the line segment joining the points A(-3, 3a + 1) and B(5, 8a) in the ratio 3: 1, find the values of a and b.
Solution:
Take (x1 , y1) = (-3, 3a + 1) ; (x2 , y2) = B(5, 8a) and
(x, y) = (-b, 9a – 2)
Here m1 = 3 and m2 =1
Question 1.
Find the mid-point of the line segment joining the points:
(i) (-6, 7) and (3, 5)
(ii) (5, -3) and (-1, 7)
Solution:
Question 2.
Points A and B have co-ordinates (3, 5) and (x, y) respectively. The mid-point of AB is (2, 3). Find the values of x and y.
Solution:
Question 3.
A (5, 3), B (-1, 1) and C (7, -3) are the vertices of triangle ABC. If L is the mid-point of AB and M is the mid-point of AC, show that LM = 1/2 BC.
Solution:
Question 4.
Given M is the mid-point of AB, find the co-ordinates of:
(i) A; if M = (1, 7) and B = (-5, 10)
(ii) B; if A = (3, -1) and M = (-1, 3).
Solution:
Question 5.
P (-3, 2) is the mid-point of line segment AB as shown in the given figure. Find the co-ordinates of points A and B.
Solution:
Question 6.
In the given figure, P (4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
Solution:
Question 7.
(-5, 2), (3, -6) and (7, 4) are the vertices of a triangle. Find the lengths of its median through the vertex (3, -6)
Solution:
Let A (-5, 2), B (3, -6) and C (7, 4) be the vertices of the given triangle.
Let AD be the median through A, BE be the median through B and CF be the median through C.
We know that median of a triangle bisects the opposite side.
Question 8.
Given a line ABCD in which AB = BC = CD, B = (0, 3) and C = (1, 8). Find the co-ordinates of A and D.
Solution:
Question 9.
One end of the diameter of a circle is (-2, 5). Find the co-ordinates of the other end of it, if the centre of the circle is (2, -1).
Solution:
Question 10.
A (2, 5), B (1, 0), C (-4, 3) and D (-3, 8) are the vertices of a quadrilateral ABCD. Find the co-ordinates of the mid-points of AC and BD.
Give a special name to the quadrilateral.
Solution:
Question 11.
P (4, 2) and Q (-1, 5) are the vertices of a parallelogram PQRS and (-3, 2) are the co-ordinates of the points of intersection of its diagonals. Find the coordinates of R and S.
Solution:
Question 12.
A (-1, 0), B (1, 3) and D (3, 5) are the vertices of a parallelogram ABCD. Find the co-ordinates of vertex C.
Solution:
Question 13.
The points (2, -1), (-1, 4) and (-2, 2) are mid-points of the sides of a triangle. Find its vertices.
Solution:
Points A (-5, x), B (y, 7) and C (1, -3) are collinear (i.e., lie on the same straight line) such that AB = BC. Calculates the values of x and y.
Solution:
Question 15.
Points P (a, -4), Q (-2, b) and R (0, 2) are collinear. If Q lies between P and R, such that PR = 2QR, calculate the values of a and b.
Solution:
Question 16.
Calculate the co-ordinates of the centroid of a triangle ABC, if A = (7, -2), B = (0, 1) and C = (-1, 4).
Solution:
Question 17.
The co-ordinates of the centroid of a PQR are (2, -5). If Q = (-6, 5) and R = (11, 8); calculate the co-ordinates of vertex P.
Solution:
Let G be the centroid of DPQR whose coordinates are (2, -5) and let (x,y) be the coordinates of vertex P.
Question 18.
A (5, x), B (-4, 3) and C (y, -2) are the vertices of the triangle ABC whose centroid is the origin. Calculate the values of x and y.
Solution:
Question 1.
Given a triangle ABC in which A = (4, -4), B = (0, 5) and C = (5, 10). A point P lies on BC such that BP: PC = 3: 2. Find the length of line segment AP.
Solution:
Question 2.
A (20, 0) and B (10, -20) are two fixed points. Find the co-ordinates of a point P in AB such that: 3PB = AB. Also, find the co-ordinates of some other point Q in AB such that AB = 6AQ.
Solution:
Question 3.
A (-8, 0), B (0, 16) and C (0, 0) are the vertices of a triangle ABC. Point P lies on AB and Q lies on AC such that AP: PB = 3: 5 and AQ: QC = 3: 5. Show that: PQ = 3/8 BC.
Solution:
Question 4.
Find the co-ordinates of points of trisection of the line segment joining the point (6, -9) and the origin.
Solution:
Question 5.
A line segment joining A(-1, 5/3) and B (a, 5) is divided in the ratio 1: 3 at P, point where the line segment AB intersects the y-axis.
(i) Calculate the value of ‘a’.
(ii) Calculate the co-ordinates of ‘P’.
Solution:
Since, the line segment AB intersects the y-axis at point P, let the co-ordinates of point P be (0, y).
P divides AB in the ratio 1: 3.
Question 6.
In what ratio is the line joining A (0, 3) and B (4, -1) divided by the x-axis? Write the co-ordinates of the point where AB intersects the x-axis.
Solution:
Question 7.
The mid-point of the segment AB, as shown in diagram, is C (4, -3). Write down the co-ordinates of A and B.
Solution:
Question 8.
AB is a diameter of a circle with centre C = (-2, 5). If A = (3, -7), find
(i) the length of radius AC
(ii) the coordinates of B.
Solution:
Question 9.
Find the co-ordinates of the centroid of a triangle ABC whose vertices are:
A (-1, 3), B (1, -1) and C (5, 1)
Solution:
Question 10.
The mid-point of the line-segment joining (4a, 2b – 3) and (-4, 3b) is (2, -2a). Find the values of a and b.
Solution:
It is given that the mid-point of the line-segment joining (4a, 2b – 3) and (-4, 3b) is (2, -2a).
Question 11.
The mid-point of the line segment joining (2a, 4) and (-2, 2b) is (1, 2a + 1). Find the value of a and b.
Solution:
Mid-point of (2a, 4) and (-2, 2b) is (1, 2a + 1), therefore using mid-point formula, we have:
Question 12.
(i) Write down the co-ordinates of the point P that divides the line joining A (-4, 1) and B (17, 10) in the ratio 1: 2.
(ii) Calculate the distance OP, where O is the origin.
(iii) In what ratio does the y-axis divide the line AB?
Solution:
Question 13.
Prove that the points A (-5, 4), B (-1, -2) and C (5, 2) are the vertices of an isosceles right-angled triangle. Find the co-ordinates of D so that ABCD is a square.
Solution:
Question 14.
M is the mid-point of the line segment joining the points A (-3, 7) and B (9, -1). Find the co-ordinates of point M. Further, if R (2, 2) divides the line segment joining M and the origin in the ratio p: q, find the ratio p: q.
Solution:
Question 15.
Calculate the ratio in which the line joining A(-4, 2) and B(3, 6) is divided by point P(x, 3). Also, find
(a) x
(b) length of AP.
Solution:
Question 16.
Find the ratio in which the line 2x + y = 4 divides the line segment joining the points P(2, -2) and Q(3, 7).
Solution:
Question 17.
If the abscissa of a point P is 2. Find the ratio in which this point divides the line segment joining the point (-4, 3) and (6, 3). Al so, find the co-ordinates of point P.
Solution:
Question 18.
The line joining the points (2, 1) and (5, -8) is trisected at the points P and Q, point P lies on the line 2x – y + k = 0, find the value of k. Also, find the co-ordinates of point Q.
Solution:
Question 19.
M is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1 : 3. Find :
(a) co-ordinates of M
(b) co-ordinates of P
(c) length of BP
Solution:
Question 20.
Find the image of the point A(5, -3) under reflection in the point P(-1, 3).
Solution:
Question 21.
A(-4, 2), B(0, 2) and C(-2, -4) are the vertices of a triangle ABC. P, Q and R are mid-points of sides BC, CA and AB respectively. Show that the centroid of ∆ PQR is the same as the centroid of ∆ ABC.
Solution:
Question 22.
From (i) and (ii), we get
Centroid of a ∆ABC = Centroid of a ∆PQR