Selina Concise Mathematics Class 9 ICSE Solutions Chapter 14 - Rectilinear Figures [Quadrilaterals: Parallelogram, Rectangle, Rhombus, Square and Trapezium]

Selina Concise Mathematics Class 9 ICSE Solutions Rectilinear Figures [Quadrilaterals: Parallelogram, Rectangle, Rhombus, Square and Trapezium]

Selina ICSE Solutions for Class 9 Maths Chapter 14 Rectilinear Figures [Quadrilaterals: Parallelogram, Rectangle, Rhombus, Square and Trapezium]

Exercise 14(A)

1.The sum of the inteior angles of a polygon is four times the sum of its exterior angles. Find the number of sides in the polygon.

Solution 1:

2.The angles of a pentagon are in the ratio 4 : 8 : 6 : 4 : 5. Find each angle of the pentagon.

Solution 2:

3.One angle of a six-sided polygon is 140^o  and the other angles are equal. Find the measure of each equal angle.

Solution 3:

4.In a polygon there are 5 right angles and the remaining angles are equal to 195^o each. Find the number of sides in the polygon.

Solution 4:

In this linear equation n and k must be integer. Therefore to satisfy this equation the minimum value of k must be 6 to get n as integer.
Hence the number of sides are: 5 + 6 = 11.

5.Three angles of a seven sided polygon are 132^o each and the remaining four angles are equal. Find the value of each equal angle.

Solution 5:

6.Two angles of an eight sided polygon are 142^o and 176^o. If the remaining angles are equal to each other; find the magnitude of each of the equal angles.

Solution 6:

7.In a pentagon ABCDE, AB is parallel to DC and A : E : D = 3 : 4 : 5. Find angle E.

Solution 7:

8.AB, BC and CD are the three consecutive sides of a regular polygon. If   BAC = 15^o;  find,

(i) Each interior angle of the polygon.

(ii) Each exterior angle of the polygon.

(iii) Number of sides of the polygon.

Solution 8:

9.The ratio between an exterior angle and an interior angle of a regular polygon is 2 : 3. Find the number of sides in the polygon.

Solution 9:

10.The difference between an exterior angle of (n - 1) sided regular polygon and an exterior angle of (n + 2) sided regular polygon is 6o find the value of n.

Solution 10:

11.Two alternate sides of a regular polygon, when produced, meet at right angle. Find:

(i) The value of each exterior angle of the polygon;

(ii) The number of sides in the polygon.

Solution 11:

Exercise 14(B)

1.State, 'true' or 'false'

(i) The diagonals of a rectangle bisect each other.

(ii) The diagonals of a quadrilateral bisect each other.

(iii) The diagonals of a parallelogram bisect each other at right angle.

(iv) Each diagonal of a rhombus bisects it.

(v) The quadrilateral, whose four sides are equal, is a square.

(vi) Every rhombus is a parallelogram.

(vii) Every parallelogram is a rhombus.

(viii) Diagonals of a rhombus are equal.

(ix) If two adjacent sides of a parallelogram are equal, it is a rhombus.

(x) If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is a square.

Solution 1:

(i)True.
This is true, because we know that a rectangle is a parallelogram. So, all the properties of a parallelogram are true for a rectangle. Since the diagonals of a parallelogram bisect each other, the same holds true for a rectangle.
(ii)False
This is not true for any random quadrilateral. Observe the quadrilateral shown below.

Clearly the diagonals of the given quadrilateral do not bisect each other. However, if the quadrilateral was a special quadrilateral like a parallelogram, this would hold true.
(iii)False
Consider a rectangle as shown below.

It is a parallelogram. However, the diagonals of a rectangle do not intersect at right angles, even though they bisect each other.
(iv)True
Since a rhombus is a parallelogram, and we know that the diagonals of a parallelogram bisect each other, hence the diagonals of a rhombus too, bisect other.
(v)False
This need not be true, since if the angles of the quadrilateral are not right angles, the quadrilateral would be a rhombus rather than a square.
(vi)True

A parallelogram is a quadrilateral with opposite sides parallel and equal.
Since opposite sides of a rhombus are parallel, and all the sides of the rhombus are equal, a rhombus is a parallelogram.
(vii)False
This is false, since a parallelogram in general does not have all its sides equal. Only opposite sides of a parallelogram are equal. However, a rhombus has all its sides equal. So, every parallelogram cannot be a rhombus, except those parallelograms that have all equal sides.
(viii)False
This is a property of a rhombus. The diagonals of a rhombus need not be equal.
(ix)True
A parallelogram is a quadrilateral with opposite sides parallel and equal.
A rhombus is a quadrilateral with opposite sides parallel, and all sides equal.
If in a parallelogram the adjacent sides are equal, it means all the sides of the parallelogram are equal, thus forming a rhombus.
(x)False

Observe the above figure. The diagonals of the quadrilateral shown above bisect each other at right angles, however the quadrilateral need not be a square, since the angles of the quadrilateral are clearly not right angles.

2.In the figure, given below, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that : AMD = 90^o.

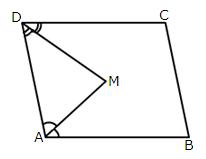
Solution 2:

3.In the following figure, AE and BC are equal and parallel and the three sides AB, CD and DE are equal to one another. If angle A is 102^o. Find angles AEC and BCD.


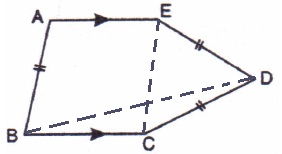
Solution 3:

4.In a square ABCD, diagonals meet at O. P is a point on BC such that OB = BP.

Show that:

i) POC =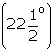 

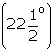
(ii) BDC = 2 POC

(iii) BOP = 3 CPO

Solution 4:

5.The given figure shows a square ABCD and an equilateral triangle ABP. Calculate:

(i) AOB

(ii) BPC

(iii) PCD

(iv) Reflex APC

Solution 5:

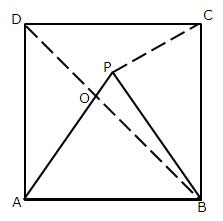
6.In the given figure ABCD is a rhombus with angle A = 67^o

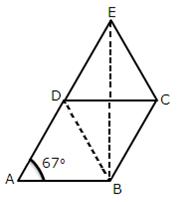
If DEC is an equilateral triangle, calculate:

(i) CBE(ii) DBE.

Solution 6:

7.In each of the following figures, ABCD is a parallelogram.

(i)

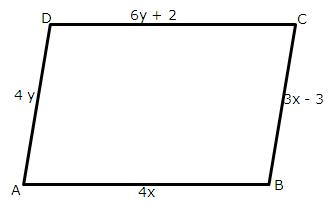
(ii)

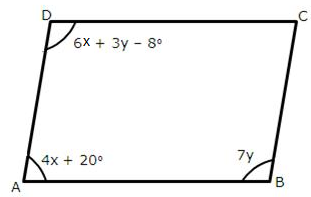
In each case, given above, find the values of x and y.

Solution 7:

8.The angles of a quadrilateral are in the ratio 3 : 4 : 5 : 6. Show that the quadrilateral is a trapezium.

Solution 8:

9.In a parallelogram ABCD, AB = 20 cm and AD = 12 cm. The bisector of angle A meets DC at E and BC produced at F. Find the length of CF.



Solution 9:

10.In parallelogram ABCD, AP and AQ are perpendiculars from vertex of obtuse angle A as shown. If  find angles of the parallelogram.

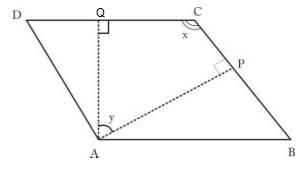
Solution 10:

We know that AQCP is a quadrilateral. So sum of all angles must be 360.
∴ x + y + 90 + 90 = 360
x + y = 180
Given x:y = 2:1
So substitute x = 2y
3y = 180
y = 60
x = 120
We know that angle C = angle A = x = 120
Angle D = Angle B = 180 – x = 180 – 120 = 60
Hence, angles of parallelogram are 120, 60, 120 and 60.

Exercise 14(C)

1.E is the mid-point of side AB and F is the mid point of side DC of parallelogram ABCD. Prove that AEFD is a parallelogram.

Solution 1:

2.The diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.

Solution 2:

3.

Solution 3:

4.In the alongside diagram, ABCD is a parallelogram in which AP bisects angle AP bisects angle A and BQ bisects angle B. Prove that :



(i) AQ = BP

(ii) PQ = CD.

(iii) ABPQ is a parallelogram.

Solution 4:

5.In the given figure, ABCD is a parallelogram. Prove that: AB = 2 BC.

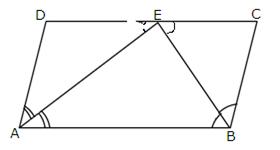
Solution 5:

NOW

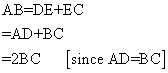
Hence proved

6.Prove that the bisectors of opposite angles of a parallelogram are parallel.

Solution 6:

7.Prove that the bisectors of interior angles of a parallelogram form a rectangle.

Solution 7:

8.Prove that the bisectors of the interior angles of a rectangle form a square.

Solution 8:

9.In parallelogram ABCD, the bisector of angle A meets DC at P and AB = 2 AD.

Prove that:

(i) BP bisects angle B.(ii) Angle APB = 90^o.

Solution 9:

10.Points M and N are taken on the diagonal AC of a parallelogram ABCD such that AM = CN. Prove that BMDN is a parallelogram.

Solution 10:

11.In the following figure, ABCD is a parallelogram. Prove that:

(i) AP bisects angle A

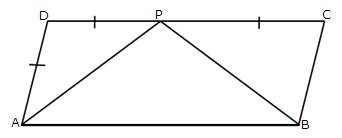
(ii) BP bisects angle B

(iii) DAP + BCP = APB

Solution 11:

12.ABCD is a square. A is joined to a point P on BC and D is joined to a point Q on AB. If AP = DQ; prove that AP and DQ are perpendicular to each other.

Solution 12:

13.In a quadrilateral ABCD, AB = AD and CB = CD. Prove that :

(i) AC bisects angle BAD.

(ii) AC is perpendicular bisector of BD.

Solution 13:

14.The following figure shows a trapezium ABCD in which AB is parallel to DC and AD = BC. Prove that:

(i) DAB = CBA

(ii) ADC = BCD

(iii) AC = BD

(iv) OA = OB and OC = OD

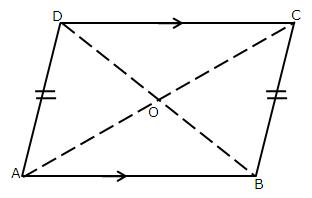
Solution 14:

15.In the given figure, AP is bisector of A and CQ is bisector of C of parallelogram ABCD. Prove that APCQ is a parallelogram.

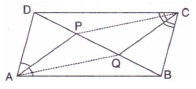
Solution 15:


16.In case of a parallelogram prove that:

(i) The bisectors of any two adjacent angles intersect at 90^o.

(ii) The bisectors of opposite angles are parallel to each other.

Solution 16:

17.The diagonals of a rectangle intersect each other at right angles. Prove that the rectangle is a square.

Solution 17:



18.In the following figure, ABCD and PQRS are two parallelograms such that ∠D = 120° and ∠Q = 70°. Find the value of x.

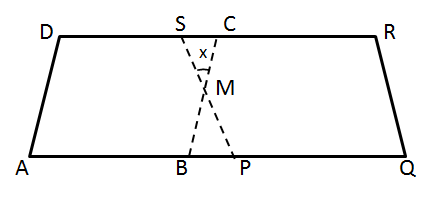
Solution 18:

19.In the following figure, ABCD is a rhombus and DCFE is a square.

 

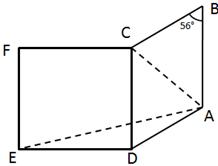
If ∠ABC =56°, find:

(i) ∠DAE

(ii) ∠FEA

(iii) ∠EAC

(iv) ∠AEC

Solution 19:

Selina Concise Mathematics Class 9 ICSE Solutions Chapter 14 - Rectilinear Figures [Quadrilaterals: Parallelogram, Rectangle, Rhombus, Square and Trapezium]