Selina Concise Mathematics Class 9 ICSE Solutions Chapter 13 - Pythagoras Theorem [Proof and Simple Applications with Converse]

Selina Concise Mathematics Class 9 ICSE Solutions Pythagoras Theorem [Proof and Simple Applications with Converse]

Selina ICSE Solutions for Class 9 Maths Chapter 13 Pythagoras Theorem [Proof and Simple Applications with Converse]

Exercise 13(A)


1.A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.

Solution 1:

2.A man goes 40 m due north and then 50 m due west. Find his distance from the starting point.

Solution 2:

3.In the figure: PSQ = 90^o, PQ = 10 cm, QS = 6 cm and RQ = 9 cm. Calculate the length of PR.

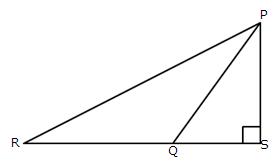
Solution 3:

4.The given figure shows a quadrilateral ABCD in which AD = 13 cm, DC = 12 cm, BC = 3 cm and ABD = BCD = 90^o. Calculate the length of AB.

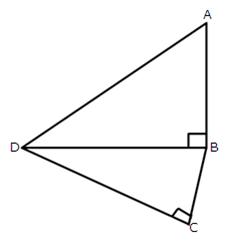
Solution 4:

5.AD is drawn perpendicular to base BC of an equilateral triangle ABC. Given BC = 10 cm, find the length of AD, correct to 1 place of decimal.

Solution 5:

6.In triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC= 3 cm. Calculate the length of OC.



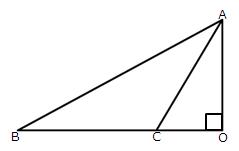
Solution 6:

7.In triangle ABC,

AB = AC = x, BC = 10 cm and the area of the triangle is 60 cm2. Find x.
Solution 7:

8.If the sides of triangle are in the ratio 1 : Selina Solutions Icse Class 9 Mathematics Chapter - Pythagoras Theorem Proof And Simple Applications With Converse: 1, show that is a right-angled triangle.

Solution 8:

9.Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m; find the distance between their tips.

Solution 9:

10.In the given figure, AB//CD, AB = 7 cm, BD = 25 cm and CD = 17 cm; find the length of side BC.

  

 

Solution 10:

Take M be the point on CD such that AB = DM.
So DM = 7cm and MC = 10 cm
Join points B and M to form the line segment BM.
So BM || AD also BM = AD.

11.In the given figure, ∠B = 90^°, XY || BC, AB = 12cm, AY = 8cm and AX: XB = 1: 2 = AY: YC. Find the lengths of AC and BC.

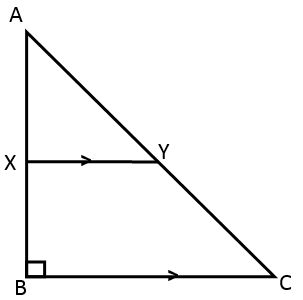
Solution 11:

Given that AX:XB = 1:2.
Let n be the common multiple for which this proportion gets satisfied.
So, AX = 1(n) and XB = 2(n)

AX = 1(n) = 4 and XB = 2(n) = 8

12.In ΔABC,  Find the sides of the triangle, if:

(i) AB = (x - 3) cm, BC = (x + 4) cm and AC = (x + 6) cm

(ii) AB = x cm, BC = (4x + 4) cm and AC = (4x + 5) cm

Solution 12:

Exercise 13(B)

1.In the figure, given below, AD  BC. Prove that: c² = a² + b² - 2ax.

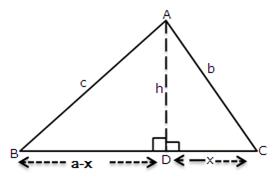
Solution 1:

2.In equilateral Δ ABC, AD  BC and BC = x cm. Find, in terms of x, the length of AD.

Solution 2:

3.ABC is a triangle, right-angled at B. M is a point on BC. Prove that:

AM² + BC² = AC² + BM².

Solution 3:

4.M andN are the mid-points of the sides QR and PQ respectively of a PQR, right-angled at Q. Prove that:

(i) PM² + RN² = 5 MN²

(ii) 4 PM² = 4 PQ² + QR²

(iii) 4 RN² = PQ² + 4 QR²

(iv) 4 (PM² + RN²) = 5 PR²

Solution 4:

5.In triangle ABC, B = 90^o and D is the mid-point of BC. Prove that: AC² = AD² + 3CD².

Solution 5:

6.In a rectangle ABCD, prove that:

AC² + BD² = AB² + BC² + CD² + DA².

Solution 6:

7.In a quadrilateral ABCD, B = 90⁰ and D = 90⁰. Prove that: 2AC² - AB² = BC² + CD² + DA²

Solution 7:

8.O is any point inside a rectangle ABCD. Prove that: OB² + OD² = OC² + OA².

Solution 8:

9.In the following figure, OP, OQ and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC. Prove that:

AR² + BP² + CQ² = AQ² + CP² + BR²

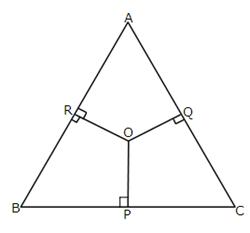
Solution 9:

10.Diagonals of rhombus ABCD intersect each other at point O. Prove that:

OA² + OC² = 2AD² - 

Solution 10:

11.In the figure AB = BC and AD is perpendicular to CD. Prove that:

AC² = 2BC. DC.

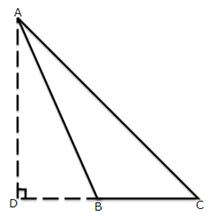
Solution 11:

12.In an isosceles triangle ABC; AB = AC and D is point on BC produced. Prove that:
AD² = AC² + BD.CD.

Solution 12:

13.In triangle ABC, angle A = 90^o, CA = AB and D is point on AB produced. Prove that DC² -BD² = 2AB.AD.

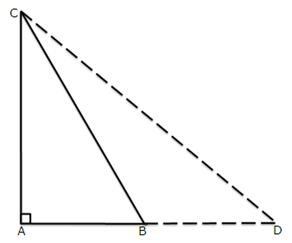
Solution 13:

14.In triangle ABC, AB = AC and BD is perpendicular to AC. Prove that: BD² - CD² = 2CD × AD.

Solution 14:

15.In the following figure, AD is perpendicular to BC and D divides BC in the ratio 1: 3.

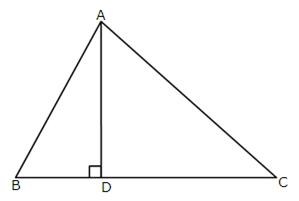
Prove that : 2AC² = 2AB² + BC²

Solution 15:

Selina Concise Mathematics Class 9 ICSE Solutions Chapter 13 - Pythagoras Theorem [Proof and Simple Applications with Converse]