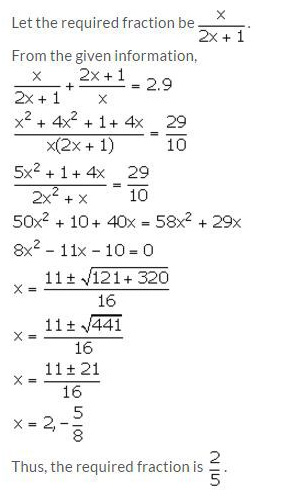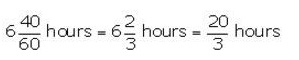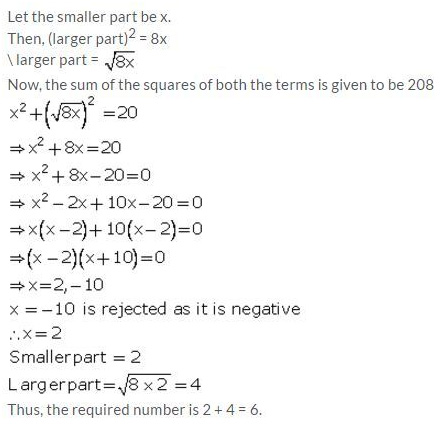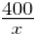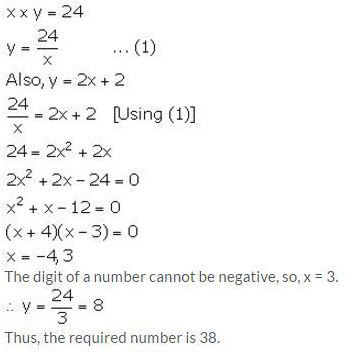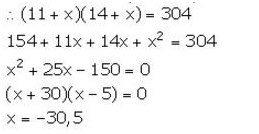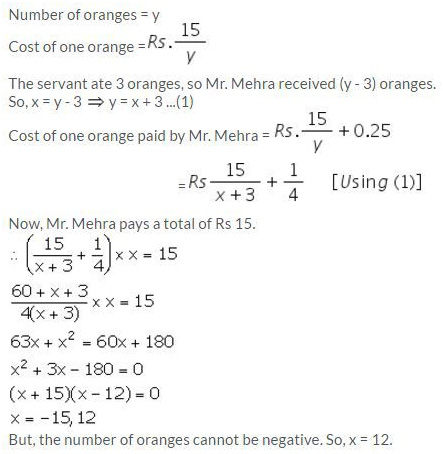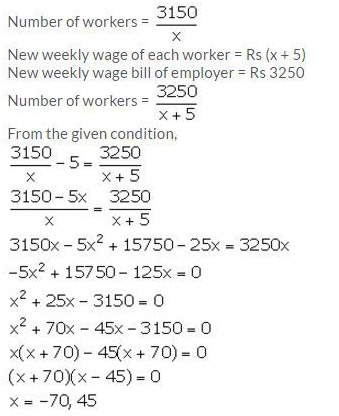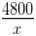Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 - Solving Simple Problems (Based on Quadratic Equations)

Selina Concise Mathematics Class 10 ICSE Solutions Solving Simple Problems (Based on Quadratic Equations)

Selina Publishers Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Simple Problems (Based on Quadratic Equations)

Solving Simple Problems (Based on Quadratic Equations) Exercise 6A – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.

The product of two consecutive integers is 56. Find the integers.

Solution:

Let the two consecutive integers be x and x + 1.

From the given information,

x(x + 1) = 56

x2 + x – 56 = 0

(x + 8) (x – 7) = 0

x = -8 or 7

Thus, the required integers are – 8 and -7; 7 and 8.

Question 2.
The sum of the squares of two consecutive natural numbers is 41. Find the numbers.

Solution:

Let the numbers be x and x + 1.

From the given information,

x2 + (x + 1)2 = 41

2x2 + 2x + 1 – 41 = 0

x2 + x – 20 = 0

(x + 5) (x – 4) = 0

x = -5, 4

But, -5 is not a natural number. So, x = 4.

Thus, the numbers are 4 and 5.

Question 3.

Find the two natural numbers which differ by 5 and the sum of whose squares is 97.

Solution:

Let the two numbers be x and x + 5.

From the given information,

x2 + (x + 5)2 = 97

2x2 + 10x + 25 – 97 = 0

2x2 + 10x – 72 = 0

x2 + 5x – 36 = 0

(x + 9) (x – 4) = 0

x = -9 or 4

Since, -9 is not a natural number. So, x = 4.

Thus, the numbers are 4 and 9.

Question 4.

The sum of a number and its reciprocal is 4.25. Find the number.

Solution:

Question 5.

Two natural numbers differ by 3. Find the numbers, if the sum of their reciprocals is

Solution:

Question 6.

Divide 15 into two parts such that the sum of their reciprocals is

Solution:

Question 7.

The sum of the square of two positive integers is 208. If the square of larger number is 18 times the smaller number, find the numbers.

Solution:

Let the two numbers be x and y, y being the bigger number. From the given information,

x2 + y2 = 208 ….. (i)

y2 = 18x ….. (ii)

From (i), we get y2=208 – x2. Putting this in (ii), we get,

208 – x2 = 18x

⇒ x2 + 18x – 208 = 0

⇒ x2 + 26X – 8X – 208 = 0

⇒ x(x + 26) – 8(x + 26) = 0

⇒ (x – 8)(x + 26) = 0

⇒ x can’t be a negative number , hence x = 8

⇒ Putting x = 8 in (ii), we get y2 = 18 x 8=144

⇒ y = 12, since y is a positive integer

Hence, the two numbers are 8 and 12.

Question 8.

The sum of the squares of two consecutive positive even numbers is 52. Find the numbers.

Solution:

Let the consecutive positive even numbers be x and x + 2.

From the given information,

x2 + (x + 2)2 = 52

2x2 + 4x + 4 = 52

2x2 + 4x – 48 = 0

x2 + 2x – 24 = 0

(x + 6) (x – 4) = 0

x = -6, 4

Since, the numbers are positive, so x = 4.

Thus, the numbers are 4 and 6.

Question 9.

Find two consecutive positive odd numbers, the sum of whose squares is 74.

Solution:

Let the consecutive positive odd numbers be x and x + 2.

From the given information,

x2 + (x + 2)2 = 74

2x2 + 4x + 4 = 74

2x2 + 4x – 70 = 0

x2 + 2x – 35 = 0

(x + 7)(x – 5) = 0

x = -7, 5

Since, the numbers are positive, so, x = 5.

Thus, the numbers are 5 and 7.

Question 10.

The denominator of a fraction is one more than twice the numerator. If the sum of the fraction and its reciprocal is 2.9; find the fraction.

Solution:

Question 11.

Three positive numbers are in the ratio 1/2 : 1/3 : 1/4. Find the numbers if the sum of their squares is 244.

Solution:

Given, three positive numbers are in the ratio 1/2 : 1/3 : 1/4 = 6 : 4 : 3

Let the numbers be 6x, 4x and 3x.

From the given information,

(6x)2 + (4x)2 + (3x)2 = 244

36x2 + 16x2 + 9x2 = 244

61x2 = 244

x2 = 4

x = ± 2

Since, the numbers are positive, so x = 2.

Thus, the numbers are 12, 8 and 6.

Question 12.
Divide 20 into two parts such that three times the square of one part exceeds the other part by 10.

Solution:

Let the two parts be x and y.

From the given information,

x + y = 20 ⇒ y = 20 – x

3x2 = (20 – x) + 10

3x2 = 30 – x

3x2 + x – 30 = 0

3x2 – 9x + 10x – 30 = 0

3x(x – 3) + 10(x – 3) = 0

(x – 3) (3x + 10) = 0

x = 3, -10/3

Since, x cannot be equal to -10/3, so, x = 3.

Thus, one part is 3 and other part is 20 – 3 = 17.

Question 13.

Three consecutive natural numbers are such that the square of the middle number exceeds the difference of the squares of the other two by 60.

Assume the middle number to be x and form a quadratic equation satisfying the above statement. Hence; find the three numbers.

Solution:

Let the numbers be x – 1, x and x + 1.

From the given information,

x2 = (x + 1)2 – (x – 1)2 + 60

x2 = x2 + 1 + 2x – x2 – 1 + 2x + 60

x2 = 4x + 60

x2 – 4x – 60 = 0

(x – 10) (x + 6) = 0

x = 10, -6

Since, x is a natural number, so x = 10.

Thus, the three numbers are 9, 10 and 11.

Question 14.

Out of three consecutive positive integers, the middle number is p. If three times the square of the largest is greater than the sum of the squares of the other two numbers by 67; calculate the value of p.

Solution:

Let the numbers be p – 1, p and p + 1.

From the given information,

3(p + 1)2 = (p – 1)2 + p2 + 67

3p2 + 6p + 3 = p2 + 1 – 2p + p2 + 67

p2 + 8p – 65 = 0

(p + 13)(p – 5) = 0

p = -13, 5

Since, the numbers are positive so p cannot be equal to -13.

Thus, p = 5.

Question 15.

A can do a piece of work in ‘x’ days and B can do the same work in (x + 16) days. If both working together can do it in 15 days; calculate ‘x’.

Solution:

Question 16.

One pipe can fill a cistern in 3 hours less than the other. The two pipes together can fill the cistern in 6 hours 40 minutes. Find the time that each pipe will take to fill the cistern.

Solution:

Let one pipe fill the cistern in x hours and the other fills it in (x – 3) hours.

Given that the two pipes together can fill the cistern in 6 hours 40 minutes, i.e.,

So, x = 15.

Thus, one pipe fill the cistern in 15 hours and the other fills in (x – 3) = 15 – 3 = 12 hours.

Question 17.

A positive number is divided into two parts such that the sum of the squares of the two parts is 20. The square of the larger part is 8 times the smaller part. Taking x as the smaller part of the two parts, find the number.

Solution:

Solving Simple Problems (Based on Quadratic Equations) Exercise 6B – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.

The sides of a right-angled triangle containing the right angle are 4x cm and (2x – 1) cm. If the area of the triangle is 30 cm²; calculate the lengths of its sides.

Solution:

Question 2.

The hypotenuse of a right-angled triangle is 26 cm and the sum of other two sides is 34 cm. Find the lengths of its sides.

Solution:

Hypotenuse = 26 cm

The sum of other two sides is 34 cm.

So, let the other two sides be x cm and (34 – x) cm.

Using Pythagoras theorem,

(26)2 = x2 + (34 – x)2

676 = x2 + x2 + 1156 – 68x

2x2 – 68x + 480 = 0

x2 – 34x + 240 = 0

x2 – 10x – 24x + 240 = 0

x(x – 10) – 24(x – 10) = 0

(x – 10) (x – 24) = 0

x = 10, 24

When x = 10, (34 – x) = 24

When x = 24, (34 – x) = 10

Thus, the lengths the three sides of the right-angled triangle are 10 cm, 24 cm and 26 cm.

Question 3.

The sides of a right-angled triangle are (x – 1) cm, 3x cm and (3x + 1) cm. Find:

(i) the value of x,

(ii) the lengths of its sides,

(iii) its area.

Solution:

Longer side = Hypotenuse = (3x + 1) cm

Lengths of other two sides are (x – 1) cm and 3x cm.

Using Pythagoras theorem,

(3x + 1)2 = (x – 1)2 + (3x)2

9x2 + 1 + 6x = x2 + 1 – 2x + 9x2

x2 – 8x = 0

x(x – 8) = 0

x = 0, 8

But, if x = 0, then one side = 3x = 0, which is not possible.

So, x = 8

Thus, the lengths of the sides of the triangle are (x – 1) cm = 7 cm, 3x cm = 24 cm and (3x + 1) cm = 25 cm.

Area of the triangle = ½ × 7 cm × 24 cm = 84 cm²

Question 4.

The hypotenuse of a right-angled triangle exceeds one side by 1 cm and the other side by 18 cm; find the lengths of the sides of the triangle.

Solution:

Let one hypotenuse of the triangle be x cm.

From the given information,

Length of one side = (x – 1) cm

Length of other side = (x – 18) cm

Using Pythagoras theorem,

x2 = (x – 1)2 + (x – 18)2

x2 = x2 + 1 – 2x + x2 + 324 – 36x

x2 – 38x + 325 = 0

x2 – 13x – 25x + 325 = 0

x(x – 13) – 25(x – 13) = 0

(x – 13) (x – 25) = 0

x = 13, 25

When x = 13, x – 18 = 13 – 18 = -5, which being negative, is not possible.

So, x = 25

Thus, the lengths of the sides of the triangle are x = 25 cm, (x – 1) = 24 cm and (x – 18) = 7 cm.

Question 5.

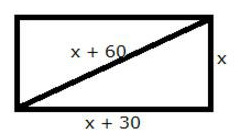
The diagonal of a rectangle is 60 m more than its shorter side and the larger side is 30 m more than the shorter side. Find the sides of the rectangle.

Solution:

Let the shorter side be x m.

Length of the other side = (x + 30) m

Length of hypotenuse = (x + 60) m

Using Pythagoras theorem,

(x + 60)2 = x2 + (x + 30)2

x2 + 3600 + 120x = x2 + x2 + 900 + 60x

x2 – 60x – 2700 = 0

x2 – 90x + 30x – 2700 = 0

x(x – 90) + 30(x – 90) = 0

(x – 90) (x + 30) = 0

x = 90, -30

But, x cannot be negative. So, x = 90.

Thus, the sides of the rectangle are 90 m and (90 + 30) m = 120 m.

Question 6.

The perimeter of a rectangle is 104 m and its area is 640 m². Find its length and breadth.

Solution:

Let the length and the breadth of the rectangle be x m and y m.

Perimeter = 2(x + y) m

∴ 104 = 2(x + y)

x + y = 52

y = 52 – x

Area = 640 m2

∴ xy = 640

x(52 – x) = 640

x2 – 52x + 640 = 0

x2 – 32x – 20x + 640 = 0

x(x – 32) – 20 (x – 32) = 0

(x – 32) (x – 20) = 0

x = 32, 20

When x = 32, y = 52 – 32 = 20

When x = 20, y = 52 – 20 = 32

Thus, the length and breadth of the rectangle are 32 cm and 20 cm.

Question 7.

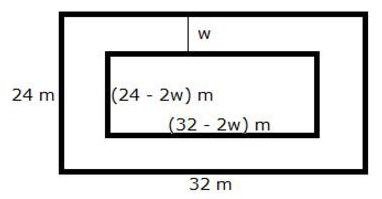
A footpath of uniform width runs round the inside of a rectangular field 32 m long and 24 m wide. If the path occupies 208 m², find the width of the footpath.

Solution:

Let w be the width of the footpath.

Area of the path = Area of outer rectangle – Area of inner rectangle

∴ 208 = (32)(24) – (32 – 2w)(24 – 2w)

208 = 768 – 768 + 64w + 48w – 4w2

4w2 – 112w + 208 = 0

w2 – 28w + 52 = 0

w2 – 26w – 2w + 52 = 0

w(w – 26) – 2(w – 26) = 0

(w – 26) (w – 2) = 0

w = 26, 2

If w = 26, then breadth of inner rectangle = (24 – 52) m = -28 m, which is not possible.

Hence, the width of the footpath is 2 m.

Question 8.

Two squares have sides x cm and (x + 4) cm. The sum of their area is 656 sq. cm. Express this as an algebraic equation in x and solve the equation to find the sides of the squares.

Solution:

Given that, two squares have sides x cm and (x + 4) cm.

Sum of their area = 656 cm2

∴ x2 + (x + 4)2 = 656

x2 + x2 + 16 + 8x = 656

2x2 + 8x – 640 = 0

x2 + 4x – 320 = 0

x2 + 20x – 16x – 320 = 0

x(x + 20) – 16(x + 20) = 0

(x + 20) (x – 16) = 0

x = -20, 16

But, x being side, cannot be negative.

So, x = 16

Thus, the sides of the two squares are 16 cm and 20 cm.

Question 9.

The dimensions of a rectangular field are 50 m and 40 m. A flower bed is prepared inside this field leaving a gravel path of uniform width all around the flower bed. The total cost of laying the flower bed and gravelling the path at Rs 30 and Rs 20 per square metre, respectively, is Rs 52,000. Find the width of the gravel path.

Solution:

Let the width of the gravel path be w m.

Length of the rectangular field = 50 m

Breadth of the rectangular field = 40 m

Let the length and breadth of the flower bed be x m and y m respectively.

Therefore, we have:

x + 2w = 50 … (1)

y + 2w = 40 … (2)

Also, area of rectangular field = 50 m 40 m = 2000 m2

Area of the flower bed = xy m2

Area of gravel path = Area of rectangular field – Area of flower bed = (2000 – xy) m2

Cost of laying flower bed + Gravel path = Area x cost of laying per sq. m

52000 = 30 xy + 20 (2000 – xy)

52000 = 10xy + 40000

xy = 1200

Using (1) and (2), we have:

(50 – 2w) (40 – 2w) = 1200

2000 – 180w + 4w2 = 1200

4w2 – 180w + 800 = 0

w2 – 45w + 200 = 0

w2 – 5w – 40w + 200 = 0

w(w – 5) – 40(w – 5) = 0

(w – 5) (w – 40) = 0

w = 5, 40

If w = 40, then x = 50 – 2w = -30, which is not possible.

Thus, the width of the gravel path is 5 m.

Question 10.

An area is paved with square tiles of a certain size and the number required is 128. If the tiles had been 2 cm smaller each way, 200 tiles would have been needed to pave the same area. Find the size of the larger tiles.

Solution:

Let the size of the larger tiles be x cm.

Area of larger tiles = x2 cm2

Number of larger tiles required to pave an area is 128.

So, the area needed to be paved = 128 x2 cm2 …. (1)

Size of smaller tiles = (x – 2)cm

Area of smaller tiles = (x – 2)2 cm2

Number of larger tiles required to pave an area is 200.

So, the area needed to be paved = 200 (x – 2)2 cm2 …. (2)

Therefore, from (1) and (2), we have:

128 x2 = 200 (x – 2)2

128 x2 = 200x2 + 800 – 800x

72x2 – 800x + 800 = 0

9x2 – 100x + 100 = 0

9x2 – 90x – 10x + 100 = 0

9x(x – 10) – 10(x – 10) = 0

(x – 10)(9x – 10) = 0

Hence, the size of the larger tiles is 10 cm.

Question 11.

A farmer has 70 m of fencing, with which he encloses three sides of a rectangular sheep pen; the fourth side being a wall. If the area of the pen is 600 sq. m, find the length of its shorter side.

Solution:

Let the length and breadth of the rectangular sheep pen be x and y respectively.

From the given information,

x + y + x = 70

2x + y = 70 … (1)

Also, area = xy = 600

Using (1), we have:

x (70 – 2x) = 600

70x – 2x2 = 600

2x2 – 70x + 600 = 0

x2 – 35x + 300 = 0

x2 – 15x – 20x + 300 = 0

x(x – 15) – 20(x – 15) = 0

(x – 15)(x – 20) = 0

x = 15, 20

If x = 15, then y = 70 – 2x = 70 – 30 = 40

If x = 20, then y = 70 – 2x = 70 – 40 = 30

Thus, the length of the shorter side is 15 m when the longer side is 40 m. The length of the shorter side is 20 m when the longer side is 30 m.

Question 12.

A square lawn is bounded on three sides by a path 4 m wide. If the area of the path isthat of the lawn, find the dimensions of the lawn.

Solution:

Let the side of the square lawn be x m.

Area of the square lawn = x2 m2

The square lawn is bounded on three sides by a path which is 4 m wide.

Area of outer rectangle = (x + 4) (x + 8) = x2 + 12x + 32

Area of path = x2 + 12x + 32 – x2 = 12x + 32

From the given information, we have:

Since, x cannot be negative. So, x = 16 m.

Thus, each side of the square lawn is 16 m.

Question 13.

The area of a big rectangular room is 300 m². If the length were decreased by 5 m and the breadth increased by 5 m; the area would be unaltered. Find the length of the room.

Solution:

Let the original length and breadth of the rectangular room be x m and y m respectively.

Area of the rectangular room = xy = 300

⇒ y =…..(1)

New length = (x – 5) m

New breadth = (y + 5) m

New area = (x – 5) (y + 5) = 300 (given)

Using (1), we have:

  

But, x cannot be negative. So, x = 20.

Thus, the length of the room is 20 m.

Solving Simple Problems (Based on Quadratic Equations) Exercise 6C – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.

The speed of an ordinary train is x km per hr and that of an express train is (x + 25) km per hr.

(i) Find the time taken by each train to cover 300 km.

(ii) If the ordinary train takes 2 hrs more than the express train; calculate speed of the express train.

Solution:

(i) Speed of ordinary train = x km/hr

Speed of express train = (x + 25) km/hr

Distance = 300 km

(ii) Given that the ordinary train takes 2 hours more than the express train to cover the distance.

Therefore,

But, speed cannot be negative. So, x = 50.

∴ Speed of the express train = (x + 25) km/hr = 75 km/hr

Question 2.

If the speed of a car is increased by 10 km per hr, it takes 18 minutes less to cover a distance of 36 km. Find the speed of the car.

Solution:

Let the speed of the car be x km/hr.

Distance = 36 km

From the given information, we have:

But, speed cannot be negative. So, x = 30.

Hence, the original speed of the car is 30 km/hr.

Question 3.

If the speed of an aeroplane is reduced by 40 km/hr, it takes 20 minutes more to cover 1200 km. Find the speed of the aeroplane.

Solution:

Let the original speed of the aeroplane be x km/hr.

But, speed cannot be negative. So, x = 400.

Thus, the original speed of the aeroplane is 400 km/hr.

Question 4.

A car covers a distance of 400 km at a certain speed. Had the speed been 12 km/h more, the time taken for the journey would have been 1 hour 40 minutes less. Find the original speed of the car.

Solution:

Let x km/h be the original speed of the car.

We know that,

It is given that the car covers a distance of 400 km with the speed of x km/h.

Thus, the time taken by the car to complete 400 km is

t = 
Now, the speed is increased by 12 km.

∴ Increased speed = (x + 12) km/hr.

Also given that, increasing the speed of the car will decrease the time taken by 1 hour 40 minutes.

Question 5.

A girl goes to her friend’s house, which is at a distance of 12 km. She covers half of the distance at a speed of x km/hr and the remaining distance at a speed of (x + 2) km/hr. If she takes 2 hrs 30 minutes to cover the whole distance, find ‘x’.

Solution:

Question 6.

A car made a run of 390 km in ‘x’ hours. If the speed had been 4 km/hour more, it would have taken 2 hours less for the journey. Find ‘x’.

Solution:

Question 7.

A goods train leaves a station at 6 p.m., followed by an express train which leaved at 8 p.m. and travels 20 km/hour faster than the goods train. The express train arrives at a station, 1040 km away, 36 minutes before the goods train. Assuming that the speeds of both the train remain constant between the two stations; calculate their speeds.

Solution:

Let the speed of goods train be x km/hr. So, the speed of express train will be (x + 20) km/hr.

Distance = 1040 km

It is given that the express train arrives at a station 36 minutes before the goods train. Also, the express train leaves the station 2 hours after the goods train. This means that the express train arrives at the stationbefore the goods train.

Since, the speed cannot be negative. So, x = 80.

Thus, the speed of goods train is 80 km/hr and the speed of express train is 100 km/hr.

Question 8.

A man bought an article for Rs x and sold it for Rs 16. If his loss was x per cent, find the cost price of the article.

Solution:

C.P. of the article = Rs x

S.P. of the article = Rs 16

Loss = Rs (x – 16)

We know:

Thus, the cost price of the article is Rs 20 or Rs 80.

Question 9.

A trader bought an article for Rs x and sold it for Rs 52, thereby making a profit of (x – 10) per cent on his outlay. Calculate the cost price.

Solution:

C.P. of the article = Rs x

S.P. of the article = Rs 52

Profit = Rs (52 – x)

We know:

Since, C.P. cannot be negative. So, x = 40.

Thus, the cost price of the article is Rs 40.

Question 10.

By selling a chair for Rs 75, Mohan gained as much per cent as its cost. Calculate the cost of the chair.

Solution:

Let the C.P. of the chair be Rs x

S.P. of chair = Rs 75

Profit = Rs (75 – x)

We know:

But, C.P. cannot be negative. So, x = 50.

Hence, the cost of the chair is Rs 50.

Solving Simple Problems (Based on Quadratic Equations) Exercise 6D – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.

The sum S of n successive odd numbers starting from 3 is given by the relation n(n + 2). Determine n, if the sum is 168.

Solution:

From the given information, we have:

n(n + 2) = 168

n² + 2n – 168 = 0

n² + 14n – 12n – 168 = 0

n(n + 14) – 12(n + 14) = 0

(n + 14) (n – 12) = 0

n = -14, 12

But, n cannot be negative.

Therefore, n = 12.

Question 2.

A stone is thrown vertically downwards and the formula d = 16t² + 4t gives the distance, d metres, that it falls in t seconds. How long does it take to fall 420 metres?

Solution:

From the given information,

16t2 + 4t = 420

4t2 + t – 105 = 0

4t2 – 20t + 21t – 105 = 0

4t(t – 5) + 21(t – 5) = 0

(4t + 21)(t – 5) = 0

t = -21/4, 5

But, time cannot be negative.

Thus, the required time taken is 5 seconds.

Question 3.

The product of the digits of a two digit number is 24. If its unit’s digit exceeds twice its ten’s digit by 2; find the number.

Solution:

Let the ten’s and unit’s digit of the required number be x and y respectively.

From the given information,

Question 4.

The product of the digits of a two digit number is 24. If its unit’s digit exceeds twice its ten’s digit by 2; find the number.

Solution:

The ages of two sisters are 11 years and 14 years.

Let in x number of years the product of their ages be 304.

But, the number of years cannot be negative. So, x = 5.

Hence, the required number of years is 5 years.

Question 5.

One year ago, a man was 8 times as old as his son. Now his age is equal to the square of his son’s age. Find their present ages.

Solution:

Let the present age of the son be x years.

∴ Present age of man = x2 years

One year ago,

Son’s age = (x – 1) years

Man’s age = (x2 – 1) years

It is given that one year ago; a man was 8 times as old as his son.

∴ (x2 – 1) = 8(x – 1)

x2 – 8x – 1 + 8 = 0

x2 – 8x + 7 = 0

(x – 7) (x – 1) = 0

x = 7, 1

If x = 1, then x2 = 1, which is not possible as father’s age cannot be equal to son’s age.

So, x = 7.

Present age of son = x years = 7 years

Present age of man = x2 years = 49 years

Question 6.

The age of the father is twice the square of the age of his son. Eight years hence, the age of the father will be 4 years more than three times the age of the son. Find their present ages.

Solution:

Let the present age of the son be x years.

Present age of father = 2x2 years

Eight years hence,

Son’s age = (x + 8) years

Father’s age = (2x2 + 8) years

It is given that eight years hence, the age of the father will be 4 years more than three times the age of the son.

2x2 + 8 = 3(x + 8) +4

2x2 + 8 = 3x + 24 +4

2x2 – 3x – 20 = 0

2x2 – 8x + 5x – 20 = 0

2x(x – 4) + 5(x – 4) = 0

(x – 4) (2x + 5) = 0

x = 4, -5/2

But, the age cannot be negative, so, x = 4.

Present age of son = 4 years

Present age of father = 2(4)2 years = 32 years

Question 7.

The speed of a boat in still water is 15 km/hr. It can go 30 km upstream and return downstream to the original point in 4 hours 30 minutes. Find the speed of the stream.

Solution:

Let the speed of the stream be x km/hr.

∴ Speed of the boat downstream = (15 + x) km/hr

Speed of the boat upstream = (15 – x) km/hr

But, x cannot be negative, so, x = 5.

Thus, the speed of the stream is 5 km/hr.

Question 8.

Mr. Mehra sends his servant to the market to buy oranges worth Rs 15. The servant having eaten three oranges on the way. Mr. Mehra pays Rs 25 paise per orange more than the market price.

Taking x to be the number of oranges which Mr. Mehra receives, form a quadratic equation in x. Hence, find the value of x.

Solution:

Question 9.

Rs 250 is divided equally among a certain number of children. If there were 25 children more, each would have received 50 paise less. Find the number of children.

Solution:

Let the number of children be x.

It is given that Rs 250 is divided amongst x students.

Since, the number of students cannot be negative, so, x = 100.

Hence, the number of students is 100.

Question 10.

An employer finds that if he increased the weekly wages of each worker by Rs 5 and employs five workers less, he increases his weekly wage bill from Rs 3,150 to Rs 3,250. Taking the original weekly wage of each worker as Rs x; obtain an equation in x and then solve it to find the weekly wages of each worker.

Solution:

Original weekly wage of each worker = Rs x

Original weekly wage bill of employer = Rs 3150

Since, wage cannot be negative, x = 45.

Thus, the original weekly wage of each worker is Rs 45.

Question 11.

A trader bought a number of articles for Rs 1,200. Ten were damaged and he sold each of the remaining articles at Rs 2 more than what he paid for it, thus getting a profit of Rs 60 on whole transaction.

Taking the number of articles he bought as x, form an equation in x and solve it.

Solution:

Number of articles bought by the trader = x

It is given that the trader bought the articles for Rs 1200.

Number of articles cannot be negative. So, x = 100.

Question 12.

The total cost price of a certain number of identical articles is Rs 4800. By selling the articles at Rs 100 each, a profit equal to the cost price of 15 articles is made. Find the number of articles bought.

Solution:

Let the number of articles bought be x.

Total cost price of x articles = Rs 4800

Cost price of one article = Rs
Selling price of each article = Rs 100

Selling price of x articles = Rs 100x

Given, Profit = C.P. of 15 articles

∴ 100x – 4800 = 15 ×
100x2 – 4800x = 15 4800

x2 – 48x – 720 = 0

x2 – 60x + 12x – 720 = 0

x(x – 60) + 12(x – 60) = 0

(x – 60) (x + 12) = 0

x = 60, -12

Since, number of articles cannot be negative. So, x = 60.

Thus, the number of articles bought is 60.

Solving Simple Problems (Based on Quadratic Equations) Exercise 6E – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.

The distance by road between two towns A and B is 216 km, and by rail it is 208 km. A car travels at a speed of x km/hr and the train travels at a speed which is 16 km/hr faster than the car. Calculate:

(i) the time taken by the car to reach town B from A, in terms of x;

(ii) the time taken by the train to reach town B from A, in terms of x.

(iii) If the train takes 2 hours less than the car, to reach town B, obtain an equation in x and solve it.

(iv) Hence, find the speed of the train.

Solution:

Question 2.

A trader buys x articles for a total cost of Rs 600.

(i) Write down the cost of one article in terms of x.

If the cost per article were Rs 5 more, the number of articles that can be bought for Rs 600 would be four less.

(ii) Write down the equation in x for the above situation and solve it for x.

Solution:

Question 3.

A hotel bill for a number of people for overnight stay is Rs 4800. If there were 4 people more, the bill each person had to pay, would have reduced by Rs 200. Find the number of people staying overnight.

Solution:

Question 4.

An Aero plane travelled a distance of 400 km at an average speed of x km/hr. On the return journey, the speed was increased by 40 km/hr. Write down an expression for the time taken for:

(i) the onward journey;

(ii) the return journey.

If the return journey took 30 minutes less than the onward journey, write down an equation in x and find its value.

Solution:

Question 5.

Rs 6500 was divided equally among a certain number of persons. Had there been 15 persons more, each would have got Rs 30 less. Find the original number of persons.

Solution:

Question 6.

A plane left 30 minutes later than the schedule time and in order to reach its destination 1500 km away in time, it has to increase its speed by 250 km/hr from its usual speed. Find its usual speed.

Solution:

Question 7.

Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels 5 km/hr faster than the second train. If after 2 hours, they are 50 km apart, find the speed of each train.

Solution:

Question 8.

The sum S of first n even natural numbers is given by the relation S = n(n + 1). Find n, if the sum is 420.

Solution:

S = n(n + 1)

Given, S = 420

n(n + 1) = 420

n2 + n – 420 = 0

n2 + 21n – 20n – 420 = 0

n(n + 21) – 20(n + 21) = 0

(n + 21) (n – 20) = 0

n = -21, 20

Since, n cannot be negative.

Hence, n = 20.

Question 9.

The sum of the ages of a father and his son is 45 years. Five years ago, the product of their ages (in years) was 124. Determine their present ages.

Solution:

Let the present ages of father and his son be x years and (45 – x) years respectively.

Five years ago,

Father’s age = (x – 5) years

Son’s age = (45 – x – 5) years = (40 – x) years

From the given information, we have:

(x – 5) (40 – x) = 124

40x – x2 – 200 + 5x = 124

x2 – 45x +324 = 0

x2 – 36x – 9x +324 = 0

x(x – 36) – 9(x – 36) = 0

(x – 36) (x – 9) = 0

x = 36, 9

If x = 9,

Father’s age = 9 years, Son’s age = (45 – x) = 36 years

This is not possible.

Hence, x = 36

Father’s age = 36 years

Son’s age = (45 – 36) years = 9 years

Question 10.

In an auditorium, seats were arranged in rows and columns. The number of rows was equal to the number of seats in each row. When the number of rows was doubled and the number of seats in each row was reduced by 10, the total number of seats increased by 300. Find:

(i) the number of rows in the original arrangement.

(ii) the number of seats in the auditorium after re-arrangement.

Solution:

Let the number of rows in the original arrangement be x.

Then, the number of seats in each row in original arrangement = x

Total number of seats = x × x = x²

From the given information,

2x(x – 10) = x2 + 300

2x2 – 20x = x2 + 300

x2 – 20x – 300 = 0

(x – 30) (x + 10) = 0

x = 30, -10

Since, the number of rows or seats cannot be negative. So, x = 30.

(i) The number of rows in the original arrangement = x = 30

(ii) The number of seats after re-arrangement = x2 + 300 = 900 + 300 = 1200

Question 11.

Mohan takes 16 days less than Manoj to do a piece of work. If both working together can do it in 15 days, in how many days will Mohan alone complete the work?

Solution:

Question 12.

Two years ago, a man’s age was three times the square of his son’s age. In three years time, his age will be four times his son’s age. Find their present ages.

Solution:

Let the age of son 2 years ago be x years.

Then, father’s age 2 years ago = 3x2 years

Present age of son = (x + 2) years

Present age of father = (3x2 + 2) years

3 years hence:

Son’s age = (x + 2 + 3) years = (x + 5) years

Father’s age = (3x2 + 2 + 3) years = (3x2 + 5) years

From the given information,

3x2 + 5 = 4(x + 5)

3x2 – 4x – 15 = 0

3x2 – 9x + 5x – 15 = 0

3x(x – 3) + 5(x – 3) = 0

(x – 3) (3x + 5) = 0

x = 3,

Since, age cannot be negative. So, x = 3.

Present age of son = (x + 2) years = 5 years

Present age of father = (3x2 + 2) years = 29 years

Question 13.

In a certain positive fraction, the denominator is greater than the numerator by 3. If 1 is subtracted from the numerator and the denominator both, the fraction reduces by. Find the fraction.

Solution:

Question 14.

In a two digit number, the ten’s digit is bigger. The product of the digits is 27 and the difference between two digits is 6. Find the number.

Solution:

Given, the difference between two digits is 6 and the ten’s digit is bigger than the unit’s digit.

So, let the unit’s digit be x and ten’s digit be (x + 6).

From the given condition, we have:

x(x + 6) = 27

x² + 6x – 27 = 0

x² + 9x – 3x – 27 = 0

x(x + 9) – 3(x + 9) = 0

(x + 9) (x – 3) = 0

x = -9, 3

Since, the digits of a number cannot be negative. So, x = 3.

Unit’s digit = 3

Ten’s digit = 9

Thus, the number is 93.

Question 15.

Some school children went on an excursion by a bus to a picnic spot at a distance of 300 km. While returning, it was raining and the bus had to reduce its speed by 5 km/hr and it took two hours longer for returning. Find the time taken to return.

Solution:

Question 16.

Rs.480 is divided equally among ‘x’ children. If the number of children were 20 more, then each would have got Rs.12 less. Find ‘x’.

Solution:

Question 17.

A bus covers a distance of 240 km at a uniform speed. Due to heavy rain its speed gets reduced by 10 km/h and as such it takes two hrs longer to covers the total distance. Assuming the uniform speed to be ‘x’ km/h, form an equation and solve it to evaluate ‘x’.

Solution:

Question 18.

The sum of the ages of Vivek and his younger brother Amit is 47 years. The product of their ages in years is 550. Find their ages.

Solution:

Given that he sum of the ages of Vivek and his younger brother Amit is 47 years.

Let the age of Vivek = x

⇒ the age of Amit = 47 – x

The product of their ages in years is 550 …. given

⇒ x(47 – x) = 550

⇒ 47x – x2 = 550

⇒ x2 – 47x + 550 = 0

⇒ x2 – 25x – 22x  + 550 = 0

⇒ x(x – 25) – 22(x – 25) = 0

⇒ (x – 25) (x – 22) = 0

⇒ x = 25 or x = 22

Given that Vivek is an elder brother.

∴ x = 25 years = age of Vivek and

age of Amit = 47 – 25 = 22 years

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 - Solving Simple Problems (Based on Quadratic Equations)