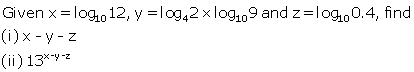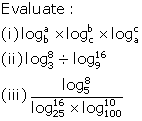Selina Concise Mathematics Class 9 ICSE Solutions Chapter 8 - Logarithms

Selina Concise Mathematics Class 9 ICSE Solutions Logarithms

Selina ICSE Solutions for Class 9 Maths Chapter 8 Logarithms

Exercise 8(A)


1.Express each of the following in logarithmic form:

(i) 5³ = 125

(ii) 3^-2 =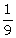 

(iii) 10^-3 = 0.001

(iv)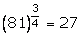 

Solution 1:

2.Express each of the following in exponential form:

(i) log_g 0.125 = -1

(ii) log₁₀0.01 = -2

(iii) log_aA = x

(iv) log₁₀1 = 0

Solution 2:

3.Solve for x: log₁₀ x = -2.

Solution 3:

4.Find the logarithm of:

(i) 100 to the base 10

(ii) 0.1 to the base 10

(iii) 0.001 to the base 10

(iv) 32 to the base 4

(v) 0.125 to the base 2

(vi) 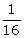 to the base 4

(vii) 27 to the base 9

(viii) 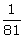 to the base 27

Solution 4:

5.State, true or false:

(i) If log₁₀ x = a, then 10^x = a.

(ii) If x^y = z, then y = log_zx.

(iii) log₂ 8 = 3 and log₈ = 2 = .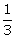

Solution 5:

6.Find x, if:

(i) log₃ x = 0

(ii) log_x 2 = -1

(iii) log₉243 = x

(iv) log₅ (x - 7) = 1

(v) log₄32 = x - 4

(vi) log₇ (2x² - 1) = 2

Solution 6:

7.Evaluate:

(i) log₁₀ 0.01

(ii) log₂ (1 ÷ 8)

(iii) log₅ 1

(iv) log₅ 125

(v) log₁₆ 8

(vi) log_0.5 16

Solution 7:

8.If log_a m = n, express a^{n - 1} in terms in terms of a and m.

Solution 8:

9.

 

Solution 9:

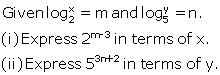
10.
 

Solution 10:

11.

Solution 11:

12.If log (x² - 21) = 2, show that x = ± 11.

Solution 12:

Exercise 8(B)

1.Express in terms of log 2 and log 3:

(i) log 36 (ii) log 144 (iii) log 4.5

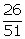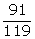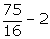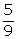(iv) log  - log  (v) log  log  + log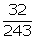 

Solution 1:

2.Express each of the following in a form free from logarithm:

(i) 2 log x - log y = 1

(ii) 2 log x + 3 log y = log a

(iii) a log x - b log y = 2 log 3

Solution 2:

3.Evaluate each of the following without using tables:

(i) log 5 + log 8 - 2 log 2

(ii) log₁₀8 + log₁₀25 + 2 log₁₀3 - log₁₀18

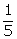(iii) log 4 + log 125 - log 32

Solution 3:

4.Prove that:

Solution 4:

5.Find x, if:

x - log 48 + 3 log 2 = 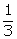log 125 - log 3.

Solution 5:

6.Express log₁₀2 + 1 in the form of log₁₀x.

Solution 6:

7.Solve for x:

(i) log₁₀ (x - 10) = 1

(ii) log (x² - 21) = 2

(iii) log (x - 2) + log (x + 2) = log 5

(iv) log (x + 5) + log (x - 5)

= 4 log 2 + 2 log 3

Solution 7:

8.Solve for x:

(i)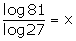 

(ii)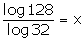 

(iii)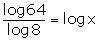 

(iv)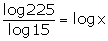 

Solution 8:

9.Given log x = m + n and log y = m - n, express the value oflog in terms of m and n.

Solution 9:

10.State, true or false:

(i) log 1 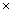log 1000 = 0

(ii)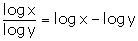 

(iii) If 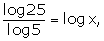then x = 2

(iv) log x 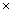log y = log x + log y

Solution 10:

11.If log₁₀2 = a and log₁₀3 = b; express each of the following in terms of 'a' and 'b':

(i) log 12(ii) log 2.25(iii) log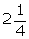 

(iv) log 5.4(v) log 60(iv) log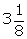 

Solution 11:

12.If log 2 = 0.3010 and log 3 = 0.4771; find the value of:

(i) log 12(ii) log 1.2(iii) log 3.6

(iv) log 15(v) log 25(vi) 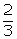log 8

Solution 12:

13.Given 2 log₁₀ x + 1 = log₁₀ 250, find :

(i) x(ii) log₁₀ 2x

Solution 13:

14.


Solution 14:

15.

Solution 15:

16.


Solution 16:

Exercise 8(C)

1.If log₁₀ 8 = 0.90; find the value of:

(i) log₁₀ 4(ii) log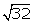 

(iii) log 0.125

Solution 1:

2.If log 27 = 1.431, find the value of :

(i) log 9 (ii) log 300

Solution 2:

3.If log₁₀ a = b, find 10^{3b - 2} in terms of a.

Solution 3:

4.If log₅ x = y, find 5^{2y+ 3} in terms of x.

Solution 4:

5.Given: log₃ m = x and log₃ n = y.

(i) Express 3^{2x - 3} in terms of m.

(ii) Write down 3^{1 - 2y + 3x} in terms of m and n.

(iii) If 2 log₃ A = 5x - 3y; find A in terms of m and n.

Solution 5:

6.Simplify:

(i) log (a)³ - log a

(ii) log (a)³ 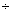 log a

Solution 6:

7.If log (a + b) = log a + log b, find a in terms of b.

Solution 7:

8.Prove that:

(i) (log a)² - (log b)² = log 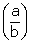. Log (ab)

(ii) If a log b + b log a - 1 = 0, then b^a. a^b = 10

Solution 8:

9.(i) If log (a + 1) = log (4a - 3) - log 3; find a.

(ii) If 2 log y - log x - 3 = 0, express x in terms of y.

(iii) Prove that: log₁₀ 125 = 3(1 - log₁₀2).

Solution 9:

10.



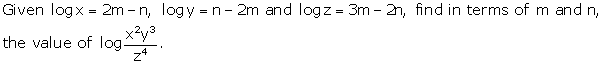
Solution 10:

11.

Solution 11:

Exercise 8(D)

1.If log a + log b - 1 = 0, find the value of a⁹.b⁴.

Solution 1:

2.If x = 1 + log 2 - log 5, y = 2 log3 and z = log a - log 5; find the value of a if x + y = 2z.

Solution 2:

3.If x = log 0.6; y = log 1.25 and z = log 3 - 2 log 2, find the values of:

(i) x+y- z        (ii) 5^{x + y - z}

Solution 3:

4.If a² = log x, b³ = log y and 3a² - 2b³ = 6 log z, express y in terms of x and z.

Solution 4:

5.If log (log a + log b), show that: a² + b² = 6ab.

Solution 5:

6.If a² + b² = 23ab, show that:

log 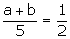(log a + log b).

Solution 6:

7.If m = log 20 and n = log 25, find the value of x, so that: 2 log (x - 4) = 2 m - n.

Solution 7:

8.Solve for x and y ; if x > 0 and y > 0;log xy = log + 2 log 2 = 2.

Solution 8:

9.Find x, if:

(i) log_x 625 = -4 

(ii) log_x (5x - 6) = 2

Solution 9:

10.
 

Solution 10:

11.

Solution 11:

12.

 

Solution 12:

13.Given log₁₀x = 2a and log₁₀y = .

(i) Write 10^a in terms of x.

(ii) Write 10^{2b + 1} in terms of y.

(iii) If , express P in terms of x and y.

Solution 13:

14.Solve:

log₅(x + 1) - 1 = 1 + log₅(x - 1).

Solution 14:

15.Solve for x, if:

Solution 15:

16.
 

Solution 16:

17.

Solution 17:

18.


Solution 18:

19.

 

Solution 19:

20.

 

Solution 20:

Selina Concise Mathematics Class 9 ICSE Solutions Chapter 8 - Logarithms