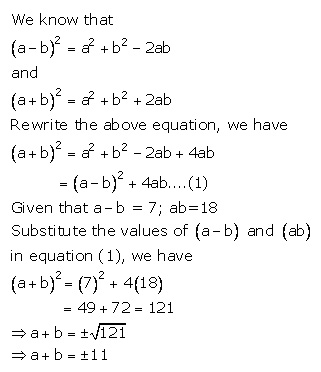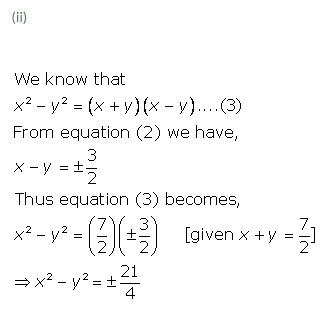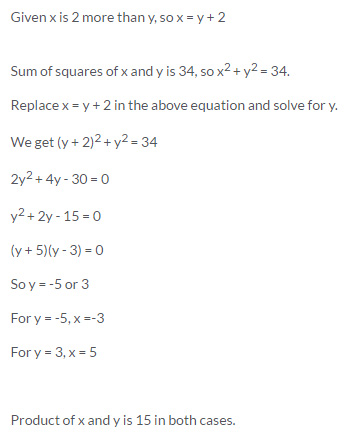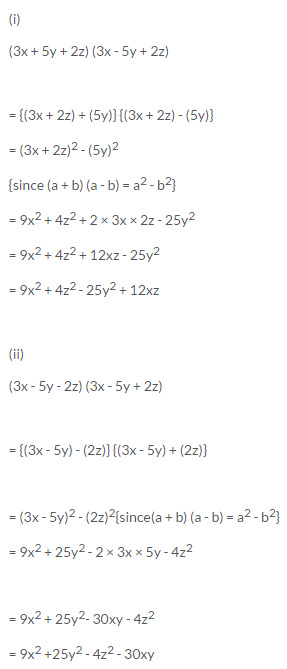Selina Concise Mathematics Class 9 ICSE Solutions Chapter 4 - Expansions (Including Substitution)

Selina Concise Mathematics Class 9 ICSE Solutions Expansions (Including Substitution)

Selina ICSE Solutions for Class 9 Maths Chapter 4 Expansions (Including Substitution)

Exercise 4(A)

1.Find the square of:

(i) 2a + b

(ii) 3a + 7b

(iii) 3a - 4b

(iv)  

Solution 1:

2.Use identities to evaluate:

(i) (101)²

(ii) (502)²

(iii) (97)²

(iv) (998)²

Solution 2:

3.Evalute:

(i)

(ii) 

Solution 3:

4.Evaluate:

(i)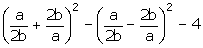 

 (ii) (4a +3b)² - (4a - 3b)² + 48ab.

Solution 4:

5.If a + b = 7 and ab = 10; find a - b.

Solution 5:

6.If a -b = 7 and ab = 18; find a + b.

Solution 6:

7.If x + y = and xy = ; find:

(i) x - y

(ii) x²- y²

Solution 7:

8.If a - b = 0.9 and ab = 0.36; find:

(i) a + b

(ii) a2 - b2.

Solution 8:

9.If a - b = 4 and a + b = 6; find

(i) a2 + b2

(ii) ab

Solution 9:

10.If a + = 6 ans  a ≠ 0 find :

(i)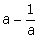 

(ii)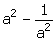 

Solution 10:

11.If a - = 8 and a ≠0, find :

(i)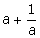 

(ii)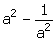 

Solution 11:

12.If a - = 8 and a ≠0, find :

(i)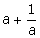 

(ii)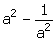 

Solution 12:

13.If a² - 5a - 1 = 0 and a ≠ 0; find:

(i) 

(ii)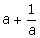 

Solution 13:

14.If 3x + 4y = 16 and xy = 4; find the value of 9x2 + 16y2.

Solution 14:

15.The number x is 2 more than the number y. If the sum of the squares of x and y is 34, then find the product of x and y.

Solution 15:

16.The difference between two positive numbers is 5 and the sum of their squares is 73. Find the product of these numbers.

Solution 16:

Exercise 4(B)

1.Find the cube of :

(i) 3a- 2b



(ii) 5a + 3b



(iii)  

(iv)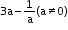   

Solution 1:

2.If a² + = 47 and a ≠ 0 find:

(i)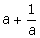 

(ii)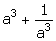 

Solution 2:

3.If a² + = 18; a ≠ 0 find:

(i)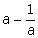 

(ii)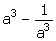 

Solution 3:

4.If a + = p and a ≠ 0 ; then show that:

Solution 4:

5.If a + 2b = 5; then show that:

a³ + 8b³ + 30ab = 125.

Solution 5:

6.If
 
_{and a ≠ 0;} 
 then show: 

a³ + 

Solution 6:

7.If a + 2b + c = 0; then show that:

a3 + 8b3 + c3 = 6abc.

Solution 7:

8.Use property to evaluate:

(i) 133 + (-8)3 + (-5)3

(ii)73 + 33 + (-10)3

(iii) 93 - 53 - 43

(iv) 383 + (-26)3 + (-12)3

Solution 8:

9.

Solution 9:

10.If  and a - 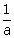= 4; find:

(i) 

(ii) 

(iii)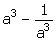 

Solution 10:

11.If and  x + 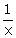= 2; then show that:

Solution 11:

12.If 2x - 3y = 10 and xy = 16; find the value of 8x3 - 27y3.

Solution 12:

13.Expand :

(i)  (3x + 5y + 2z) (3x - 5y + 2z)

(ii)  (3x - 5y - 2z) (3x - 5y + 2z)

Solution 13:

14.The sum of two numbers is 9 and their product is 20. Find the sum of their

(i) Squares (ii) Cubes

Solution 14:

15.Two positive numbers x and y are such that x > y. If the difference of these numbers is 5 and their product is 24, find:
(i) Sum of these numbers
(ii) Difference of their cubes
(iii) Sum of their cubes.

Solution 15:

Exercise 4(C)

1.Expand:

(i) (x + 8) (x + 10)

(ii) (x + 8) (x - 10)

(iii) (x - 8) (x + 10)

(iv) (x - 8) (x - 10) 

Solution 1:

2.

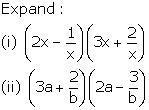Solution 2:

3.

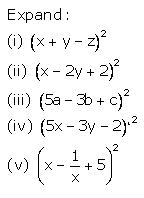Solution 3:

4.If a + b + c = 12 and a2 + b2 + c2 = 50; find ab + bc + ca.

Solution 4:

5.If a2 + b2 + c2 = 35 and ab + bc + ca = 23; find a + b + c.

Solution 5:

6.If a + b + c = p and ab + bc + ca = q; find a2 + b2 + c2.


Solution 6:

7.If a2 + b2 + c2 = 50 and ab + bc + ca = 47, find a + b + c.

Solution 7:

8.If x+ y - z = 4 and x2 + y2 + z2 = 30, then find the value of xy - yz - zx.

Solution 8:

Exercise 4(D)



1.If x + 2y + 3z = 0 and x³ + 4y³ + 9z³ = 18xyz; evaluate:

Solution 1:

2.If a + = m and a ≠ 0 ; find in terms of 'm'; the value of :

(i)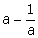 

(ii)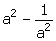 

Solution 2:

3.In the expansion of (2x² - 8) (x - 4)²; find the value of

(i) coefficient of x³

(ii) coefficient of x²

(iii) constant term.

Solution 3:

4.
If x > 0 and
 
find: 


Solution 4:

5.If 2(x² + 1) = 5x, find :

(i) 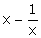(ii) 

Solution 5:

6.If a² + b² = 34 and ab = 12; find:

(i) 3(a + b)² + 5(a - b)²

(ii) 7(a - b)² - 2(a + b)²

Solution 6:

7.If 3x -  _and x ≠ 0 find : 

Solution 7:

8.If x² + = 7 and  x ≠ 0; find the value of:

.

Solution 8:

9.If x = and x ≠ 5 find .

Solution 9:

10.
If x =  _and x ≠ 5 find .

Solution 10:

11.If 3a + 5b + 4c = 0, show that:

27a³ + 125b³ + 64c³ = 180 abc

Solution 11:

12.The sum of two numbers is 7 and the sum of their cubes is 133, find the sum of their square.

Solution 12:

13.In each of the following, find the value of 'a':

(i) 4x² + ax + 9 = (2x + 3)²

(ii) 4x² + ax + 9 = (2x - 3)²

(iii) 9x² + (7a - 5)x + 25 = (3x + 5)²

Solution 13:

14.
If
 

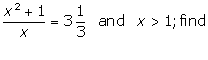
(i) 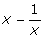 (ii) 

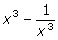
Solution 14:

15.The difference between two positive numbers is 4 and the difference between their cubes is 316.

Find:

(i) Their product

(ii) The sum of their squares

Solution 15:

Exercise 4(E)



1.Simplify:

(i) (x + 6)(x + 4)(x - 2)

(ii) (x - 6)(x - 4)(x + 2)

(iii) (x - 6)(x - 4)(x - 2)

(iv) (x + 6)(x - 4)(x - 2) 

Solution 1:

2.

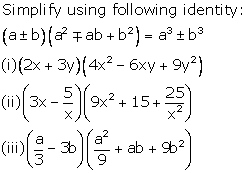Solution 2:

3.Using suitable identity, evaluate

(i) (104)³

(ii) (97)³ 

Solution 3:

4.




Solution 4:

5.

Solution 5:

6.If a - 2b + 3c = 0; state the value of a3 - 8b3 + 27c3.

Solution 6:

7.If x + 5y = 10; find the value of x3 + 125y3 + 150xy - 1000.

Solution 7:

8.

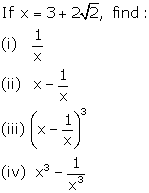
Solution 8:

9.If a + b = 11 and a2 + b2 = 65; find a3 + b3.

Solution 9:

Selina Concise Mathematics Class 9 ICSE Solutions Chapter 4 - Expansions (Including Substitution)