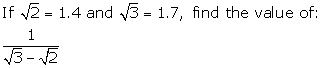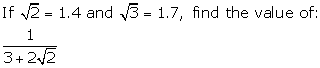Selina Concise Mathematics Class 9 ICSE Solutions Chapter 1 - Rational and Irrational Numbers

Selina Concise Mathematics Class 9 ICSE Solutions Rational and Irrational Numbers

Selina ICSE Solutions for Class 9 Maths Chapter 1  Rational and Irrational Numbers

Exercise 1(A)

1.

Solution 1:

2.

Solution 2:

3.

Solution 3:

4.

Solution 4:

5.

Solution 5:

6.

Solution 6:

7.

Solution 7:

8.

Solution 8:

9.Arrange      in ascending order of their magnitudes.

Also, find the difference between the largest and smallest of these fractions. Express this difference as a decimal fraction correct to one decimal place.

Solution 9:

10.Arrange   in descending order of their magnitudes. Also, find the sum of the lowest and largest of these fractions. Express the result obtained as a decimal fraction correct to two decimal places.

Solution 10:

Exercise 1(B)

1.

Solution 1:

2.

Solution 2:

3.(i)

Solution 3(i):

3.(ii)

Solution 3(ii):

3.(iii)

Solution 3(iii):

3.(iv)

Solution 3(iv):

3.(v)

Solution 3(v):

3.(vi)

Solution 3(vi):

3.(vii)

Solution 3(vii):

3.(viii)

Solution 3(viii):

4.

Solution 4:

5.(i)  

Solution 5(i):

5.(ii)

Solution 5(ii):

5.(iii)

Solution 5(iii):

5.(iv)

Solution 5(iv):

5.(v)

Solution 5(v):

5.(vi)



Solution 5(vi):

5.(vii)



Solution 5(vii):

5.(viii)



Solution 5(viii):

Exercise 1(C)

1.State, whether the following numbers are rational or not:
(i) (ii) (iii) 

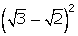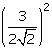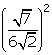
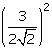(iv) (v) (vi)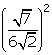 

Solution 1:

2.Find the square of:

Solution 2:

3.Selina Solutions Icse Class 9 Mathematics Chapter - Rational And Irrational Numbers

(i)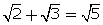 

(ii)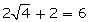 

(iii)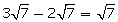 

(iv) is an irrational number

(v) is a rational number.

(vi) All rational numbers are real numbers.

(vii)All real numbers are rational numbers.

(viii) Some real numbers are rational numbers.

Solution 3:

4.Given universal set =

From the given set, find :

(i) set of rational numbers

(ii) set of irrational numbers

(iii) set of integers

(iv) set of non-negative integers

Solution 4:

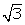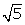5. To show that    and   are irrational numbers.

Solution 5:

6. Use method of contradiction to show that and are irrational numbers.

Solution 6:

7.Write a pair of irrational numbers whose sum is irrational.

Solution 7:

8.Write a pair of irrational numbers whose sum is rational.

Solution 8:

9.Write a pair of irrational numbers whose difference is irrational.

Solution 9:

10.Write a pair of irrational numbers whose difference is rational.

Solution 10:

11. Write a pair of irrational numbers whose product is irrational.

Solution 11:

12.

Solution 12:

13.Write in ascending order:

(i)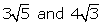 

(ii)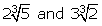 

(iii)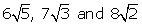 

Solution 13:

14.Write in descending order:

(i)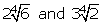 

(ii)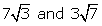 

Solution 14:

15.Compare.

Solution 15:

16.Insert two irrational numbers between 5 and 6.

Solution 16:

17.Insert five irrational numbers between and .

Solution 17:

18.Write two rational numbers between 

Solution 18:

19.Write three rational numbers between 

Solution 19:

Exercise 1(D)

1. State, with reasons, which of the following are surds and which are not:

(i)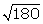 

(ii) 

(iii)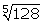 

(iv)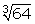 

(v)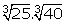 

(vi)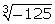 

(vii)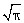 

(viii)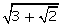 

Solution 1:

2.Write the lowest rationalising factor of:

(i)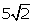 

(ii)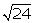 

(iii)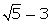 

(iv)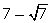 

(v)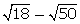 

(vi)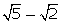 

(vii)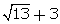 

(viii)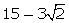 

(ix)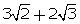 

Solution 2:

3.Rationalise the denominators of :

(i)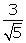 

(ii)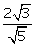 

(iii) 

(iv)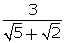 

(v)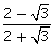 

(vi)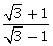 

(vii)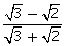 

(viii)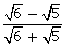 

(ix)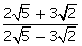 

Solution 3:

4.Find the values of 'a' and 'b' in each of the following:

(i)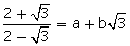 

(ii)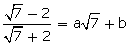 

(iii) 

(iv) 

Solution 4:

5.Simplify:

(i)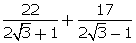 

(ii)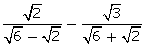 

Solution 5:

6.If= and y = ; find:

(i) x²(ii) y²

(iii) xy(iv) x² + y² + xy.

Solution 6:

7.

(i) m² 

(ii) n²

(iii) mn

Solution 7:

8.If x = 2+ 2, find:

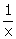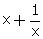(i) (ii) (iii)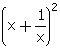 

Solution 8:

9.


Solution 9:

10.


Solution 10:

11.


Solution 11:

12.


Solution 12:

13.(i)

Solution 13(i):

13.(ii)

Solution 13(ii):

Selina Concise Mathematics Class 9 ICSE Solutions Chapter 1 - Rational and Irrational Numbers